Centro de Bachillerato Tecnológico Industrial y de Servicios 214 Chetumal, Quintana Roo
Anuncio

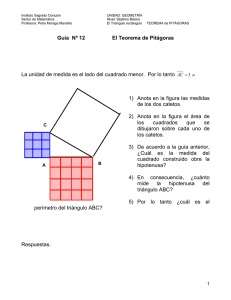
Centro de Bachillerato Tecnológico Industrial y de Servicios 214 Chetumal, Quintana Roo Nombre del alumno: …………………………………………………………Fecha: ……. Ejercicios sobre el Teorema de Pitágoras 1. Traza un triángulo rectángulo y escaleno del tamaño de tu preferencia y construye los cuadrados sobre los lados del triángulo. De una hoja del color de tu agrado, recorta un cuadrado congruente con el cuadrado construido sobre el cateto menor. De una hoja de otro color que combine con el color de la hoja anterior, recorta un cuadrado congruente con el que está construido sobre el cateto mayor y córtalo en cuatro piezas como se indica en la figura 1. Acomoda las cinco piezas que has obtenido encima del cuadrado construido sobre la hipotenusa y observa que lo cubren por completo. Figura1. El cuadrado construido sobre el cateto mayor lo descomponemos en cuatro partes de la siguiente manera: por el centro del cuadrado, es decir, el punto donde se cortan sus diagonales, trazamos una paralela a la hipotenusa y una perpendicular a este segmento. 2. Formula las expresiones algebraicas del Teorema de Pitágoras aplicando las notaciones adaptadas para las longitudes de los lados de los triángulos rectángulos de la figura 151. a) b) c) d) e) f) Figura 151. 3. ¿Cuáles de los siguientes triángulos son rectángulos? a) b) c) XY = 2.0 cm XZ = 1.2 cm YZ = 1.6 cm AC = 2 cm CB = 8 cm AB = 10 cm KM = 1.00 cm KL = 2.75 cm ML = 2.50 cm 4. Selecciona tres números de cada inciso de manera que sean las longitudes de los lados de un triángulo rectángulo. a) 10, 13, 6, 21, 5, 18, 12 b) 1, 1.2, 5.1, 0.6, 0.8, 2, 3.2 c) 3 1 2 1 5 4 7 , , ,1 , , , 4 2 3 3 6 5 8 5. Verifica si con las longitudes proporcionadas en cada inciso es posible construir un triángulo rectángulo. a) 10, 24, 26 c) 1, 1, 3 e) 2, 2, 2 2 b) 6, 8, 10 d) 2 3 , 6, 4 3 f) 7, 5, 5 6. ¿Cuál es el perímetro del triángulo rectángulo ABC de la figura 152? Figura 152.