2 - etsac-est1

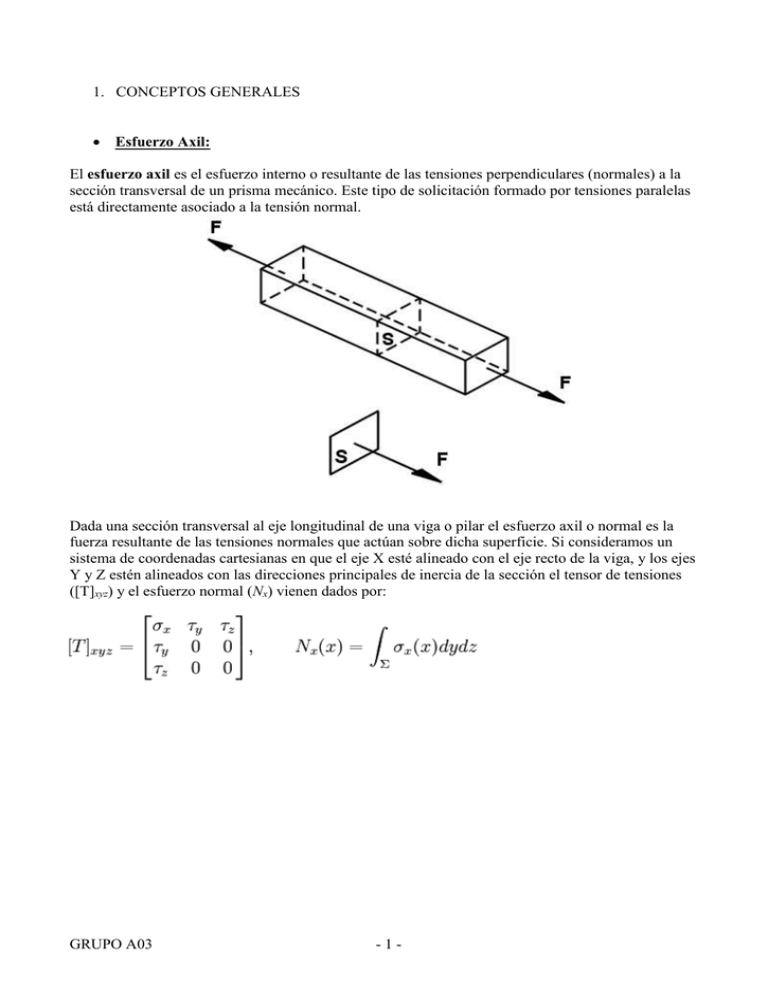
1. CONCEPTOS GENERALES
 Esfuerzo Axil:
El esfuerzo axil es el esfuerzo interno o resultante de las tensiones perpendiculares (normales) a la
sección transversal de un prisma mecánico. Este tipo de solicitación formado por tensiones paralelas
está directamente asociado a la tensión normal.
Dada una sección transversal al eje longitudinal de una viga o pilar el esfuerzo axil o normal es la
fuerza resultante de las tensiones normales que actúan sobre dicha superficie. Si consideramos un
sistema de coordenadas cartesianas en que el eje X esté alineado con el eje recto de la viga, y los ejes
Y y Z estén alineados con las direcciones principales de inercia de la sección el tensor de tensiones
([T]xyz) y el esfuerzo normal (Nx) vienen dados por:
GRUPO A03
-1-
 Pandeo
Definición:
El pandeo es un fenómeno de inestabilidad elástica que puede darse en elementos comprimidos
esbeltos, y que se manifiesta por la aparición de desplazamientos importantes transversales a la
dirección principal de compresión.
Imagen representativa:
No se debe confundir este fenómeno con las deformaciones sufridas por elementos sometidos a
esfuerzos de flexión:
Diferencias entre flexión y el pandeo. En el primer caso la flexión es ocasionada por una carga
perpendicular a la viga, mientras que en el segundo caso, se ha sometido una barra a dos fuerzas en el
sentido de su largo.
GRUPO A03
-2-
Causas del pandeo:
En el caso de barras esbeltas, debemos tener en cuenta que si la fuerza aplicada sobre una barra
“perfecta” sigue la dirección exacta del lugar geométrico de los centros de gravedad de la sección no
se producirá el pandeo. Pero en las condiciones reales en que actúa el sistema pueden existir una o más
de las siguientes causas que determina el pandeo, como por ejemplo:

Irregularidades en la forma.

Irregularidades en la estructura.

Excentricidad de la carga respecto al centroide geométrico.

Pequeña flexión del eje.
Carga Crítica. Euler.
La carga axial que da inicio a la inestabilidad por pandeo en un elemento estructural se conoce como
carga crítica de pandeo del elemento o carga de Euler. Para el análisis de Euler se considera que la
barra está articulada en ambos extremos. Se puede tomar como referencia a un elemento estructural
ideal de eje recto, sin imperfecciones del material ni de alineación del elemento, con una longitud L,
de sección constante A e inercia I, constituido por un material lineal elástico cuyo módulo de
elasticidad es E. En uno de sus extremos se coloca un apoyo fijo y en el otro, un apoyo deslizante
longitudinal.
Siendo: Pcrit, la carga crítica; E, Módulo de Young del material de que está hecha la barra; Imin,
momento de inercia mínimo de la sección transversal de la barra; L, longitud de la barra y λ la esbeltez
mecánica de la pieza.
Esta fórmula se aplica para una pieza que puede considerarse biarticulada en sus extremos. Cuando las
condiciones de sujeción de los extremos son diferentes la carga crítica de Euler viene dada por una
ecuación del tipo:
GRUPO A03
-3-
Al producto
se le llama longitud de pandeo. Lp.
Esquema con imágenes de los tipos de sujeción, y su variación correspondiente en el valor de su
longitud de pandeo:

Barras articuladas-articuladas en los extremos:
Lp = L

Barras empotradas en un extremo y libres en el otro :
Lp = 2xL

Barras empotradas en los dos extremos :
Lp =0.5L

Barras empotradas en un extremo y articulada en el otro :
Lp = 0.70.L
GRUPO A03
-4-

Barra empotrada en un extremo y empotrada monodeslizante en el otro extremo:
Lp = 0.70.L

Barra articulada-empotrada monodeslizante :
Lp = 0.70.L
GRUPO A03
-5-
2. BIBLIOGRAFÍA DE APOYO
TÍTULO:
RESISTENCIA DE MATERIALES
AUTORES:
Luis Ortiz Berrocal
EDITORIAL:
McGraw-Hill
AÑO:
1990
COMENTARIO:
Libro de amplio contenido de resistencia de materiales, dedica un capítulo
entero a la flexión lateral o pandeo, donde hay varios ejemplos visuales y nos
aporta la resolución al problema.
TÍTULO:
EL SÓLIDO ELÁSTICO EN LA ARQUITECTURA
AUTORES:
Manuel Muñoz Vidal
Emilio Martin Gutiérrez
Manuel González Crespo
Manuel Freire Tellado
EDITORIAL:
NINO
AÑO:
1998
COMENTARIO:
GRUPO A03
Libro donde se tratan diversos temas, muy completo y bastante fácil de
entender las explicaciones de los conceptos que se quieren explicar. Tiene
imágenes ilustrativas, así como nos muestran las diferentes formulas a utilizar.
-6-
TÍTULO:
MECÁNICA DE MATERIALES
AUTORES:
R.C. Hibbeler
EDITORIAL:
Prentice Hall
AÑO:
1997
COMENTARIO:
Libro muy amplio sobre la mecánica de los materiales. Tiene un formulario que
nos hace una idea para realizar uno propio para los exámenes. Buena
explicación de los conceptos ayudado con gráficos o dibujos explicativos, por
cada apartado trae ejercicios resueltos así como una buena recopilación
problemas a realizar.
TÍTULO:
ELASTICIDAD
AUTORES:
Luis Ortiz Berrocal
EDITORIAL:
McGraw-Hill
AÑO:
1998
COMENTARIO:
Este libro como bien dice su titulo trata únicamente sobre la elasticidad y su
estudio. Es un libro completo en cuanto al tema de la elasticidad aunque al
desarrollar los conceptos es algo complicado de entender sin conocimientos
previos. Tiene alguna ilustración explicativa pero la mayoría son formulas.
GRUPO A03
-7-
TÍTULO:
RESISTENCIA DE MATERIALES
AUTORES:
Fernando Rodríguez-Avial Azcunaga
EDITORIAL:
Bellisco
AÑO:
1974
COMENTARIO:
Encontramos información acerca de la resistencia de materiales, donde se
explican varios conceptos válidos para nuestro estudio. Además tiene gráficos
con los que entendemos mejor lo que quiere explicar el autor, también tiene
ejercicios para realizar. Libro algo antiguo pero nos sirve para entender los
conceptos.
GRUPO A03
-8-
3. EJEMPLO RESUELTO
Sea un soporte constituido por dos UPN 180 soldados a un perfil IPE 180 como se indica en la figura:
El conjunto tiene una altura de 3 m, un extremo del soporte se encuentra empotrado y el otro es
articulado, para todas las direcciones. Datos:
Acero S275 JR
F1  2 1350104 mm 1320104 mm4  40,2 106 mm4
2

 91
 
4
I Z  2114 10  2800   70  19,2    101 104  55,22  106
2
 

B=0,7 EN AMBAS DIRECCIONES
EJE PANDEO = EJE IMIN = EJE Y
2=C
EN AMBAS DIRECCIONES
  
  E  I Y
N CR  
 LK 
Lk  3000 0,7  2100
E  2,1  105 N 2
m
6
F1  40,2 10 mm4
N CR  18,89 106 N
GRUPO A03
-9-

A  FY
N CR
A  2  2800 2390  7990mm
FY  275
2
N CR  18,89 10 N
  0,341
6
N bRd    A  fyd
A  7990
275
fyd 
1,05
  0,94
GRUPO A03

0,30
0,34
0,40
NbRd  1,96 106 N
- 10 -

0,95

0,90
  0,94
4. FORMULARIO
N bRd    A  fyd    A 
fy
M
N bRd  Resistencia minorada a compresión (N)
  Coeficiente de reducción por pandeo  1
fyd  Límite elástico del acero minorado (N/mm2)
fy  Límite elástico del acero (N/mm2)
 M  Coeficiente parcial de seguridad relativo a los fenómenos de inestabilidad=1,05
Para calcular  necesito:

N cr     E  I
 Lk 
N cr  Axil crítico de Euler (N)
2
E  Módulo de Young  2,1 105 (N/mm2)
I=Momento de inercia de la sección con respecto al eje de pandeo a considerar (mm2)
Lk=Longitud de pandeo de la barra (mm)
Lk= L  B
L=Longitud de la barra (mm)
B=Coeficiente de esbeltez, está en función de las condiciones de enlaces.
5 TIPOS
Biempotrado
Empotrado
Articulado
B=0,5
B=0,7
GRUPO A03
Biarticulado
B=1
Mensula
B=2
- 11 -
Biempotrado
con posibilidad de
desplazamiento
transversal relativo
B=1
A  FY
2
N CR
  Esbeltez reducida
A= Área sección (mm2)
Fy=Límite elástico del acero (N/mm2)
Ncr=Axil crítico de Euler

  Coeficiente de imperfección elástico – Tablas 6.1. y 6.3.
  0,5  1     0,2  2 

1
   2  2
1
Para calcular la posibilidad de que pandee un pilar en un edificio mirar el apartado 6.3.2.5. del
documento Básico SE-AE
Los valores de  se pueden obtener directamente de la figura 6.3. o de la tabla 6.3. en función del
coeficiente de imperfección y de la esbeltez reducida.
AXILES A TRACCION
T= N /A
T = TENSION
N= AXIL
A= AREA
DIMENSIONADO
- POR RESISTENCIA
A ≥ NED / FYD
A= AREA
N= AXIL MAYORADO
FYD= LIMITE ELÁSTICO DEL ACERO MINORADO
- POR DEFORMACIÓN
A ≥ N L / E AL
A= AREA
N = AXIL
L = LONGITUD DE LA BARRA
E = MODULO DE ELASTICIDAD LONGITUDINAL
AL = VARIACIÓN DE LONGITUD
GRUPO A03
- 12 -
5. IMAGEN RESUMEN
En la imagen se aprecia un pilar estructural excéntrico al que se le ha tenido que añadir cierto volumen
de hormigón además de una pequeña ménsula también de hormigón para "reconducir" la carga de
manera que esta pase por el eje del pilar convirtiéndose en una carga axil centrada.
GRUPO A03
- 13 -