tica formación general_GUIAN°4

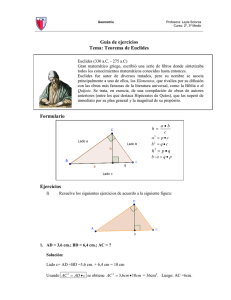
I. MUNICIPALIDAD DE PROVIDENCIA
CORPORACIÓN DE DESARROLLO SOCIAL
LICEO POLIVALENTE “ARTURO ALESSANDRI PALMA” ANº12
DEPARTAMENTO: Matemática
Mail del Departamento: Deptomatematica.a12@gmail.com
GUIA 4 3° MEDIO
SECTOR:
Matemática
Nivel 3/curso3º B-C-D-E-F-G
PROFESOR: Miguel Jofre
Plazo: 21 Noviembre
UNIDAD TEMÁTICA: Mas sobre el triángulo rectángulo
CONTENIDO: Teorema de Euclides
APRENDIZAJE ESPERADO: Aplicar las relaciones de Euclides para encontrar longitudes
NOMBRE……………………………………..CURSO.4º……. FECHA:…………..
Instrucciones: Lea los conceptos y revisa los ejemplos de cada tema y sus distinta formas de
cómo se desarrollan, luego desarrolla los ejercicios y finalmente envía la evaluación
ACTIVIDAD DE EVALUACIÓN
Fecha de entrega 21 de Noviembre de 2011-12:00
hrs. p.m.
Deptomatematica.a12@gmail.com
Teorema de Euclides.
La altura correspondiente a la hipotenusa es media proporcional entre los segmentos de la
hipotenusa.
C
A
Sea AD=q
y DB=p
D
B
CD=h entonces:
h2  p  q
Cada cateto es media proporcional entre la hipotenusa y su proyección sobre ella..
C
AC=b y
BC=a
A
D
B
a2
a2  c  p
c
de cada una de estas igualdades se tiene:
2
b2
b  cq
q
c
p
Luego volviendo a la relación inicial de Euclides se tiene:
a 2 b 2 a 2b 2
h  p  q =   2 luego al extraer raíz se tiene:
c c
c
2
h
ab
c
Ejercicios de Recapitulación:
1. . En la figura , dadas las dimensiones del rectángulo ABCD, entonces la medida del
lado BE en el rectángulo DBEF mide
(Problema extraído del ensayo Demre )
Desarrollo:
1) llamemos x al lado DE a su vez
llamaremos h.
la altura del triángulo rectángulo DCB en C la
2) En el mismo triángulo se tiene: BC=1 y CD=2 (ambos catetos) y DB la
hipotenusa la cual aplicando Pitágoras se tiene:
DB 2  12  2 2
DB  5
Luego aplicando Euclides para encontrar h se tiene:
h
ab 1 2
2
2 5



c
5
5
5
Finalmente como h=BE se tiene que BE=
2 5
5
2. . En un  ABC rectángulo en C , la proyección del cateto “a” mide 12 cm más que la
proyección del cateto “b” sobre la hipotenusa. Calcula la altura hc si mide el doble que la menor
de las proyecciones de los catetos.
C
A
Sea AD=q
y DB=p
CD=h
BC=a
B
D
AC=a
AB=c
Interpretando el enunciado se tiene p=12+q
A su vez
h=2q
El teorema de Euclides nos dice que .
h2  p  q
(2q) 2  (q  12)  q
4q 2  q 2  12q
3q 2  12q  0
q(3q  12)  0
donde q=0 lo que no puede ser ó 3q-12=0
q=4
Luego h=2q=8 cm
3.En el triángulo ABC, rectángulo en C, de la figura 12, DB  5 , BC  13 y CD  12 . La base AB mide:
Desarrollo:
Aplicando Euclides se tiene:
132  AB  5
169  5 AB
169
 AB
5
4.Según los datos de la figura , La medida de HB es:
Desarrollo Aplicando Euclides se tiene:
152  9  AB
225  9 AB
225
 AB
9
25  AB
Entonces HB =
AB -AH
HB= 25 -9 =16
ACTIVIDAD
DE APRENDIZAJE
EJERCICIO 1
En la siguiente figura AB  10 , BC  8 , determinar
AC ; AD ; DB y CD
C
A
D
B
EJERCICIO 2
En la siguiente figura DB  12 , BC  15 , determinar
C
A
D
SOLUCIONES:
B
AB ; AD ; C D y AC
AC  6; DB 
32
18
24
; AD  ; CD 
5
5
5
AB 
75
27
45
; AD 
; CD  9; AC 
4
4
4
Evaluación:
1. En la figura, se muestra la boca de un túnel con forma de semicírculo, cuyo diámetro
mide 6 metros. ¿Cuál es la máxima altura que puede tener una persona para no golpearse
con el túnel, si pasa a 60 cm. del punto B?
2En una plaza de una ciudad se encuentra un tobogán del cual solo se conoce la distancia
de los puntos que tienen contacto con el suelo como se muestra el esquema de la figura
9. A partir de esta información y la proporcionada en la misma figura , las longitudes a del
tobogán y b de la escalinata son respectivamente:
3Un albañil se encuentra diseñando el techo de una ampliación formada por una sucesión
de vigas iguales que, en su unión, forman un ángulo recto. Se baja una perpendicular
desde dicha unión sobre la viga horizontal quedan determinados dos segmentos, como
muestra la figura 10. En base a las medidas que se muestran en la misma figura , la
longitud d de la viga inclinada más largas es:
Mediante esta pauta te vamos a evaluar
Categoría
1)Aplicar
teoremas
de Euclides
y Pitágoras
Excelente
3 puntos
Reemplazar
adecuadamente y
obtener la
respuesta
correcta
Bueno
2 puntos
Reemplazar
adecuadamente y
obtener una
respuesta errónea
Regular
1 punto
Reconocer los
teoremas y reemplaza
inadecuadamente
Insuficiente
0 puntos
No reconoce lo
que debe
realizar