Interpolación lineal
Anuncio
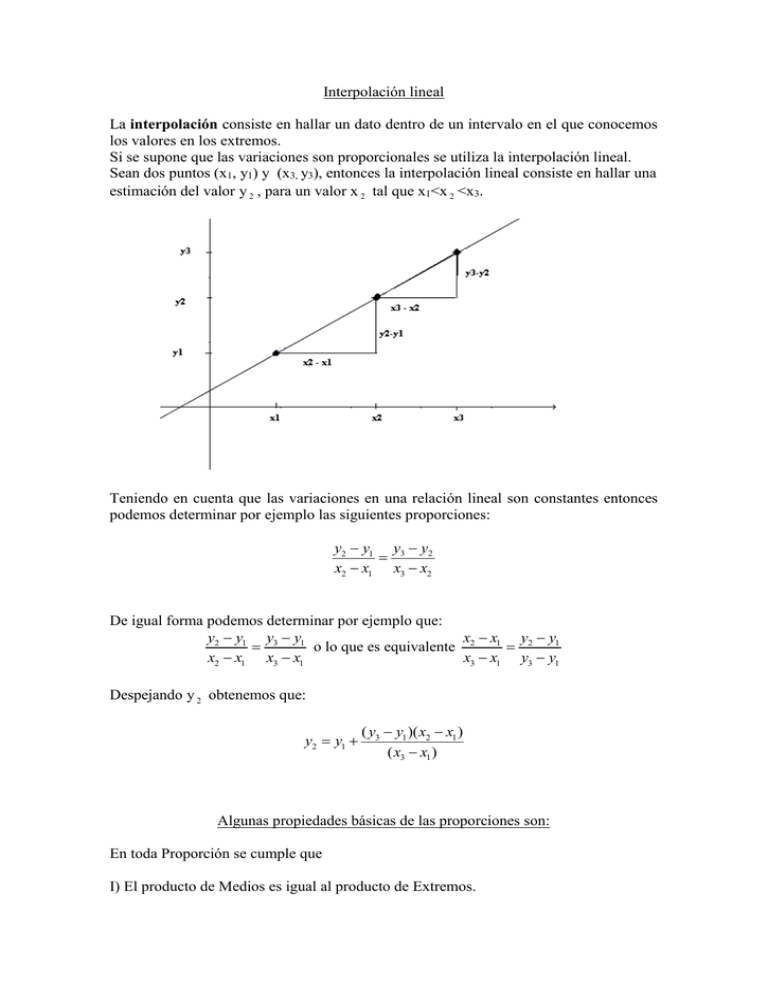
Interpolación lineal La interpolación consiste en hallar un dato dentro de un intervalo en el que conocemos los valores en los extremos. Si se supone que las variaciones son proporcionales se utiliza la interpolación lineal. Sean dos puntos (x1, y1) y (x3, y3), entonces la interpolación lineal consiste en hallar una estimación del valor y 2 , para un valor x 2 tal que x1<x 2 <x3. Teniendo en cuenta que las variaciones en una relación lineal son constantes entonces podemos determinar por ejemplo las siguientes proporciones: y2 y1 y3 y2 x2 x1 x3 x2 De igual forma podemos determinar por ejemplo que: y2 y1 y3 y1 x x y y o lo que es equivalente 2 1 2 1 x2 x1 x3 x1 x3 x1 y3 y1 Despejando y 2 obtenemos que: y2 y1 ( y3 y1 )( x2 x1 ) ( x3 x1 ) Algunas propiedades básicas de las proporciones son: En toda Proporción se cumple que I) El producto de Medios es igual al producto de Extremos. II) Alternar Extremos: III) Alternar Medios: IV) Permutar: V) Invertir: VI) Componer respecto al Antecedente y Consecuente respectivamente: VII) Descomponer respecto al Antecedente y Consecuente respectivamente: VIII) Componer y descomponer a la vez: Ejemplo de interpolación lineal (Ejercicio 2 práctico 2): Si queremos aproximadamente determinar la mediana para el tamaño de las ordenes, a través de interpolación lineal entonces podemos proceder de la siguiente manera: Tamaño de las órdenes durante el pasado año fiscal de la compañía Eliot Tamaño de.. 0,10 10,25 25,50 N° ordenes 950 de Porcentaje de ordenes 23.3 Porcentaje acumulado 23.3 940 23.1 46.4 110 2.7 49.1 50,100 100, 250 250,500 500,1000 680 16.7 65.8 260 6.4 72.2 480 11.8 84 650 16 100 Fuente: Cátedra de Estadística Observando la tabla de distribución de frecuencias vemos que el intervalo que acumula el 50% de los datos es 50,100 , por lo tanto en él está contenida la mediana. Ahora suponiendo que las frecuencias están distribuidas proporcionalmente en el intervalo: 50____________49,1 Me___________50 100__________65,8 podemos plantear por ejemplo la siguiente proporción: Me 50 50 49,1 100 50 65,8 49,1 Despejando Me 50 (100 50)(50 49,1) (65,8 49.1) 52,99 Nota: La interpolación se puede realizar tanto con las frecuencias acumuladas absolutas, como con las relativas o relativas porcentuales.











