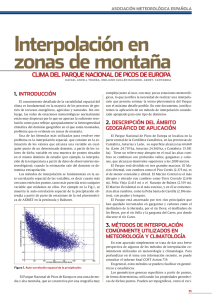
Ejemplos de Interpolación Bilineal (del Atributo) α = x - i β= y
Anuncio

Ejemplos de Interpolación Bilineal (del Atributo) Al graficar pixel a pixel un objeto 3D, se proyectan en la pantalla (coordenadas CRT) pixeles contiguos en las coordenadas normalizadas (0,0), (1,0), (0,1), (1,1) con intensidades de u= 4, 8, 2, 10, respectivamente. Se desea hacer un “zoom” del despliegue, ¿cómo determinaría la intensidad de un punto localizado en (x, y) = (0.25, 0.75)? Dé la o las fórmulas generales para calcular u en cualquier punto (x, y) que satisfaga 0 x 1 y 0 y 1. Hay varios criterios; por vecino más próximo, el pixel más cercano a (0.25, 0.75) es (0,1), cuya intensidad es u = 2. por interpolación, como hay cuatro vecinos, escogemos interpolación bilineal; tenemos valores intermedios (en el diagrama, i, j = 0,0 en nuestro caso particular): En el caso general (cualquier x,y): =xi = y j u j = (1) ui j + ui+1 j u j+1 = (1) ui j+1 + u i+1 j+1 I(x, y) = u = (1) u j + u j+1 o también (versión transpuesta): ui = (1) ui j + ui j+1 ui+1 = (1) ui+1 j + u i+1 j+1 I(x, y) = u = (1) u i + u i+1 Para 0 x 1 y 0 y 1, escogiendo la 1ª. versión (se obtiene al final el mismo valor interpolado en ambas versiones) es: =x = y u0 = (1) u00 + u10 u1 = (1) u01 + u11 I(x, y) = u = (1) u0 + u1 substituyendo (x, y) = (0.25, 0.75), y u00= 4, u10= 8, u01= 2, u11= 10: =x = y u0 = (10.25) 4 + 0.25 8 = 5 u1 = (10.25) 2 + 0.25 10 = 4 I(x, y) = u = (10.75) 5 + 0.75 4 = 4.25 Para interpolaciones de orden superior (bicúbica, polinomial, etc) se requieren de más vecinos del punto a interpolar. Nota: Si el atributo es vectorial, por ejemplo I(x,y) = u = (u1,u2,u3,u4), se realiza una interpolación bilineal por cada canal ( y son los mismos): u 0 (1 ) u 00 u10 u 0 (1 ) u 00 u10 I x, y u (1 ) u 0 u 1 Ejemplo, con atributos en color u = (r,g,b), para todos los valores de (, ) [0,1][1,0], con pixeles de (1/640)(1/480) unidades: La Interpolación Trilineal es la Extensión a 3D del Caso Bilineal. Ejercicio: encontrar las ecuaciones, para una interpolación trilineal, siendo el tercer parámetro de la última interpolación para hallar C, a partir de C1 y C0 en las figuras siguientes. El código binario de los subíndices coincide con las ocho combinaciones de offsets a partir del voxel en (i, j, k ). Suponga que C es el atributo en la posición no entera (x,y,z).