Mar de Aral - Departamento de Matemáticas
Anuncio

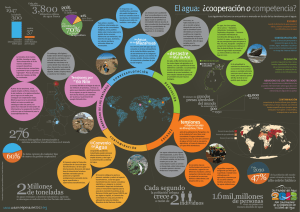
Análisis matemático de un desastre ecológico: La disminución de volumen y de superficie del Mar de Aral. Un modelo sencillo Por JMPC, para la 2ª ed. del Máster de Gestión Litoral (2008-2009) Partimos de la Figura 1, donde se ve la disminución de superficie del Mar de Aral, sólo una parte del desastre de la zona: Figura 1: La bajada del nivel del Mar de Aral dejó a casi todos los buques del lago en tierra. El problema comenzó hacia 1960 al desviarse los dos ríos que alimentaban dicho Mar para aprovechar sus aguas en el riego de campos de algodón. Al no tener otras entradas de agua, el volumen del Mar comenzó a disminuir debido a la evaporación. Con la disminución de volumen aparecen también las de profundidad y de superficie, que se aprecian en la figura 1. En el momento presente, el Mar de Aral se ha reducido a la cuarta parte de su configuración original. Para construir un modelo, supongamos una forma adecuada para el Mar de Aral, pues la relación entre volumen total y superficie libre depende del tipo de cuerpo geométrico con que identifiquemos dicho lago. No es razonable tomar un cilindro, pues la superficie libre sería siempre la misma, igual al área de la base, y vemos que en la realidad ha ido disminuyendo. Por ello supondremos (Figura 2) que el Mar de Aral 1 se representa como un cono invertido, de modo que V (t ) h(t ) S (t ) , siendo h(t ) la 3 profundidad máxima: 1 r(t) h(t) ángulo Figura 2: Geometría del modelo del Mar de Aral. También supondremos que el ángulo de apertura en el vértice es (que puede medirse mediante las curvas de nivel de un mapa) de modo que el radio de la base y la r (t ) tan . Por tanto, como el altura del cono se hallan relacionados por la fórmula h(t ) área de la base es S (t ) r (t ) 2 , el volumen vendrá dado por la expresión V (t ) 3tan r (t ) 3 , y despejando el radio en función del volumen, se tendrá 1 3 3 r (t ) V (t ) tan . Así las cosas, la superficie libre quedará en función del volumen: 2 3 S (t ) 3V (t ) tan 3tan V (t ) A *V (t ) 3 2 3 3 2 3 2 3 [1] Sólo resta, por tanto, calcular las fluctuaciones del volumen de agua del Mar de Aral. El volumen variará según la ley de balance: V (t t ) V (t ) flujo de entrada flujo de salida t donde las entradas son los aportes de los ríos que vierten al Mar y las salidas se producen por evaporación (consideramos, para simplificar, la precipitación lluviosa como despreciable). Llamando F (t ) al flujo de los ríos, y sabiendo que la cantidad de agua evaporada es proporcional a la superficie libre, se llega a: V (t t ) V (t ) F (t ) kS(t )t Dividiendo por t y tomando límites cuando este incremento tiende hacia cero, se obtiene una ecuación diferencial que, acompañada de la condición representativa del volumen inicial antes de la intervención de los ríos para el riego, nos dará el modelo siguiente: 2 V ' (t ) F (t ) kS (t ) V ( 0) V 0 [2] Sustituyendo [1] en la ecuación diferencial [2], y escribiendo A kA * , nos quedará 2 3 V ' (t ) AV (t ) F (t ) [3] Para representar F (t ) se necesita una función decreciente, y un tipo adecuado puede ser F (t ) aebt , siendo a el flujo total que vertían los ríos al Mar, antes de iniciarse su desvío, y b un parámetro positivo que indica a qué velocidad ha ido disminuyendo ese flujo. Esta ecuación no es fácil de integrar, así que la resolvemos directamente en forma numérica. Nótese ahora que para ello es necesario dar valores a las siguientes cantidades que intervienen en el modelo: , V0 , k , a, b Con una elección arbitraria de valores (se deja a Uds. la búsqueda de los valores verdaderos y poner las unidades adecuadas): 800 , V0 1, k 0.1, a 1, b 1 se obtienen las gráficas que vienen a continuación (se les invita a interpretarlas y a modificar los parámetros para practicar un poco): Volumen del Mar de Aral 1 Volumen 0,8 0,6 0,4 0,2 0 0 1 2 3 4 5 4 5 tiempo Superficie del Mar de Aral 9,6 Superficie 9,48 9,36 9,24 9,12 9 0 1 2 3 tiempo 3 Una vez hecho esto, el análisis con el modelo puede continuar con el estudio de: el aumento de la concentración de abonos de uso agrícola en el agua del Mar de Aral (no olviden que es un lago de agua dulce), la interacción de estos abonos con la fauna de peces (todas las especies originales se hallan extinguidas, aunque se ha introducido recientemente alguna nueva que parece resistir algo más…), la influencia de la cantidad de agua y su superficie libre en la regulación de la temperatura del aire, y por tanto el cambio climático, que trae consigo la disminución de la rentabilidad de los cultivos e industrias asociadas (las relacionadas con la pesca ya desaparecieron, claro), y el empobrecimiento económico, y finalmente las migraciones de la población hacia zonas con más esperanza de buena calidad de vida, etc. etc. 4