12_matematicas_iii - facultad de mecanica & energia
Anuncio

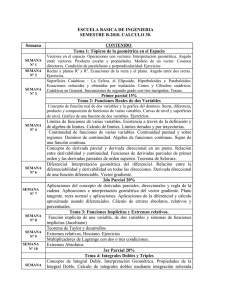
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA MECANICA-ENERGIA Av. Juan Pablo II s/n. Bellavista Callao Teléfonos: 429-9740 Anexos: 291-293-294 Telefax: 420-0217 SILABO I. INFORMACION GENERAL 1.1 NOMBRE DEL CURSO 1.2 CÓDIGO 1.3 EXTENSION HORARIA 1.4 CRÉDITOS 1.5 PRE-REQUISITO 1.6 SEMESTRE ACADEMICO 1.7 CARÁCTER Y TURNO 1.8 DURACIÓN : : : : : : : : MATEMÁTICA III M3112 Teoría: 04 h. Práctica: 02 h. 04 Matemática II 2008 - B Obligatorio y Mañana 17 semanas II. OBJETIVOS 2.1 GENERALES: Formar al estudiante en el razonamiento lógico, la capacidad del análisis y reflexión, motivando a expresarse por medio de un lenguaje preciso y riguroso de manera que sea capaz de resolver los problemas de su especialidad. Utilizar las propiedades y métodos del cálculo de varias variables a los cursos de su especialidad 2.2 ESPECIFICOS: Al concluir la asignatura el alumno será capaz de: Reconocer curvas en el espacio a través de su curvatura y torsión Gráficar funciones de varias variables Interpretar geométricamente la derivada direccional y el gradiente Resolver problemas utilizando multiplicadores de Lagrange Hallar el volumen de cualquier sólido utilizando integrales dobles y triples Interpretar la integral de línea en diferentes aspectos de la física, mecánica Interpretación física del rotacional y la divergencia de un campo vectorial. III. SUMILLA 3.1NATURALEZA DE LA ASIGNATURA: El curso pertenece al área de ciencias. 3.2 SINTESIS DE CONTENIDO: Funciones vectoriales de variable real, Funciones de varias variables, Integrales dobles, triples y múltiples. Funciones vectoriales de varias variables. Integral de línea de superficie, Teorema de Stokes y de la divergencia. IV. CRONOGRAMA. SEMANA 1. FUNCIONES VECTORIALES DE UNA VARIABLE REAL (6 horas) OBJETIVO Reconocer las curvas en el espacio a través de su curvatura y Torsión. 1.1 Función vectorial de una variable real. 1.2 Definición, Ejemplos, gráficas 1.3 Límite y continuidad. 1.4 Propiedades, Teoremas principales Practica dirigida 2 Horas = 6 Horas 7,14% SEMANA 2. (6 horas) 2.1 La derivada. Teorema. El diferencial. 2.2 IIntegración, Propiedades. Longitud de arco. 2.3 Movimiento de una curva a lo largo de una curva Practica dirigida = 12 Horas 14,28% SEMANA 3 3.1 Vector tangente, normal principal, y Binormal. 3.2 Curvatura y torsión. 3.3 Teoremas 3.4 Ejemplos y problemas de aplicación a la mecánica. 3.5 Primera Práctica Calificada = 18 Horas 21,14% 2 Horas (4 horas) Semana 4. FUNCIONES DE VARIAS VARIABLES. OBJETIVOS: Interpretar geométricamente la derivada direccional y el gradiente. Resolver problemas utilizando multiplicadores de Lagrange. Hallar el volumen de sólidos utilizando integrales dobles y triples. (2 horas) (6 horas) 4.1 Funciones reales de varias variables: Definición. Dominio y rango. Curvas y Superficies de Nivel gráfico. 4.2 Límites y continuidad de funciones de varias variables. 4.3 Derivadas parciales. Notaciones usuales. Interpretación geométrica Practica dirigida 2 Horas = 24 Horas 28,56% SEMANA 5. 5.1 Diferenciabilidad. La diferencial total. 5.2 Derivada de la función compuesta y la función implícita. 5.3 Ejemplos de aplicación Practica dirigida = 30 Horas 35,7% (6 horas) SEMANA 6. 6.1 Derivadas direccionales. Gradiente. 6.2 Plano tangente y recta normal 6.3 Derivada de orden superior . Propiedades 6.4 Segunda Práctica Calificada = 36 Horas 42,84% (4 horas) 2 Horas (2 horas) SEMANA 7. (6 horas) 7.1 Máximos y Mínimos. 7.2 El criterio de las derivadas parciales. 7.3 Máximos y mínimos condicionados. Métodos de multiplicadores de Lagrange 7.4 Problemas de aplicación Practica dirigida 2 Horas = 42 Horas 50% SEMANA 8. PRIMER EXAMEN PARCIAL SEMANA 9. INTEGRALES MULTIPLES (6 horas) OBJETIVOS: Hallar el volumen de cualquier sólido utilizando integrales dobles y triples 9.1 Introducción. 9.2 Integrales Dobles. Integrales Iteradas. Teorema fundamental. 9.3 Integrales Triples. Integrales Iteradas. Teorema fundamental. Practica dirigida = 48 Horas 57,14% SEMANA 10. 10.1 Superficies en tres dimensiones. 10.2 Coordenadas cilíndricas. 10.3 La Integral en Coordenadas Cilíndricas Practica dirigida = 54 Horas 64,28% 2 Horas (6 horas) 2 Horas SEMANA 11. FUNCIONES VECTORIALES DE VARIAS VARIABLES (4 horas) OBJETIVOS: Interpretar la integral de línea en diferentes aspectos de la física. Dar la Interpretación física del rotacional y la divergencia de un campo vectorial. 11.1 Introducción. 11.2 Limites y continuidad de funciones vectoriales de varias variables integral de línea. 11.3 El concepto de trabajo como integral de línea 11.4 Tercera Práctica Calificada (2 horas) = 60 Horas 71.42% SEMANA 12. (6 horas) 12.1 Integrales de línea con respecto a la longitud de arco. 12.2 Conjuntos conexos abiertos. 12.3 Primer y segundo teorema fundamental del cálculo para las integrales de línea. 12.4 Integral de línea independiente de la trayectoria Practica dirigida 2 Horas = 66 Horas 78.56% SEMANA 13. 13.1 Teoremas de Green en el plano. 13.2 Teorema de Green para regiones múltiplemente conexas. 13.3 Representación paramétrica de una superficie. Practica dirigida =72 Horas 85,7% (6 horas) 2 Horas SEMANA 14 . (4 horas) 14.1 Plano tangente y normal. 14.2 Area de la superficie: Representación paramétrica explícita e implícita de la superficie. 14.3 Cuarta Práctica Calificada (2 horas) = 78 Horas 92,84% SEMANA 15. 15.1 Las integrales de superficie. Teorema de Stokes 15.2 El rotacional y la divergencia de un campo vectorial 15.3 Teorema de la divergencia(Teorema de Gauss. Practica dirigida = 84 Horas 100% SEMANA 16. EXAMEN FINAL SEMANA 17. EXAMEN SUSTITUTORIO V. METODOS Y TECNICAS DE ENSEÑANZA (6 horas) 2 Horas El curso se desarrollará mediante clases teóricas - prácticas, aplicando los principios didácticos. El proceso enseñanza aprendizaje propicia la participación plena del alumno, despertando el interés al estudio sistemático en una dinámica interactiva entre el profesor y alumno. Se pretende una orientación adecuada incentivando su capacidad creadora Hacia la Formulación de modelos y a la investigación. VI. METODOS DE EVALUACIÓN El proceso de evaluación consta de cuatro (04) prácticas calificadas de las cuales se elimina el de menor puntaje y dos (02) exámenes parcial (EP) y final (EF). Además, se evaluará un tercer examen que sustituirá el examen de menor puntaje, siempre que la nota final (NF) sea mayor que 07 y menor 10.5. La nota final (NF) del curso se obtiene como sigue: NOTA FINAL NF PP EP EF 3 VII. BIBLIOGRAFIA 9.1 BIBLIOGRAFIA BASICA: 1 Grossman, S. 2 Pita Ruiz, Claudio : Multivariable Calculus Edit. Prentice Hall Hispanoamericana. S.A. 2004 : Cálculo Vectorial. Edit. Prentice Hall Hispanoamericana, S.A. México 1995 primera edición. 9.2 BIBLIOGRAFIA COMPLEMENTARIA: 1. Lasalle Sullivan, Haaser : Análisis matemático II Edit. Trillas México 1976 2 Marsden : Cálculo Vectorial Edit. Aadison, 1999. 3 Purcell, E. : Cálculo con Geometría Analítico Edit. Prentice Hall Hispanoamericana S.A.; 1998. Bellavista, setiembre 2008