Documento 406193
Anuncio
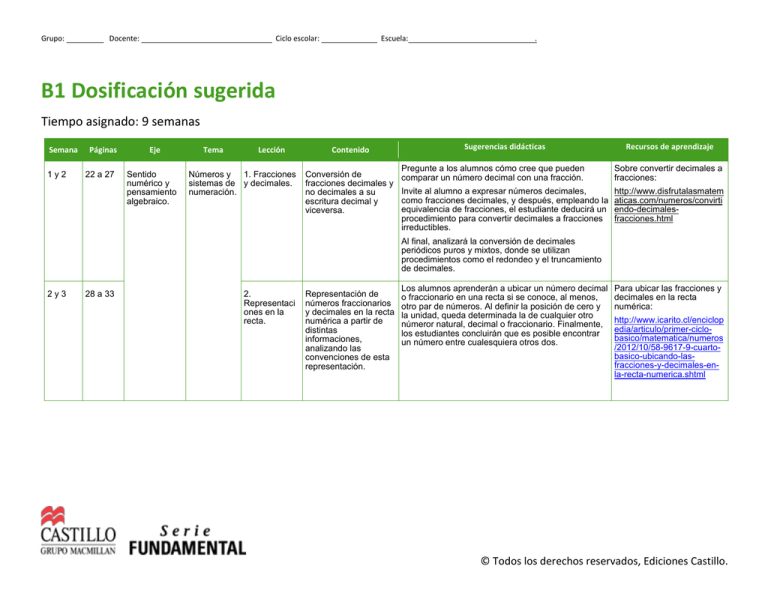
Grupo: Docente: Ciclo escolar: Escuela: . B1 Dosificación sugerida Tiempo asignado: 9 semanas Semana 1y2 Páginas 22 a 27 Eje Sentido numérico y pensamiento algebraico. Tema Lección Números y 1. Fracciones sistemas de y decimales. numeración. Contenido Conversión de fracciones decimales y no decimales a su escritura decimal y viceversa. Sugerencias didácticas Recursos de aprendizaje Pregunte a los alumnos cómo cree que pueden comparar un número decimal con una fracción. Sobre convertir decimales a fracciones: Invite al alumno a expresar números decimales, como fracciones decimales, y después, empleando la equivalencia de fracciones, el estudiante deducirá un procedimiento para convertir decimales a fracciones irreductibles. http://www.disfrutalasmatem aticas.com/numeros/convirti endo-decimalesfracciones.html Al final, analizará la conversión de decimales periódicos puros y mixtos, donde se utilizan procedimientos como el redondeo y el truncamiento de decimales. 2y3 28 a 33 2. Representaci ones en la recta. Representación de números fraccionarios y decimales en la recta numérica a partir de distintas informaciones, analizando las convenciones de esta representación. Los alumnos aprenderán a ubicar un número decimal o fraccionario en una recta si se conoce, al menos, otro par de números. Al definir la posición de cero y la unidad, queda determinada la de cualquier otro númeror natural, decimal o fraccionario. Finalmente, los estudiantes concluirán que es posible encontrar un número entre cualesquiera otros dos. Para ubicar las fracciones y decimales en la recta numérica: http://www.icarito.cl/enciclop edia/articulo/primer-ciclobasico/matematica/numeros /2012/10/58-9617-9-cuartobasico-ubicando-lasfracciones-y-decimales-enla-recta-numerica.shtml © Todos los derechos reservados, Ediciones Castillo. Grupo: Semana Docente: Páginas Ciclo escolar: Eje Tema Lección 3y4 34 a 37 Problemas aditivos. 3. Suma y resta de fracciones. 4 38 a 44 Patrones y 4. ecuaciones. Sucesiones. 5 45 a 50 5. De letras y figuras. Escuela: Contenido Resolución y planteamiento de problemas que impliquen más de una operación de suma y resta de fracciones. Construcción de sucesiones de números o de figuras a partir de una regla dada en lenguaje común. Formulación en lenguaje común de expresiones generales que definen las reglas de sucesiones con progresión aritmética o geométrica, de números y de figuras. Explicación del significado de fórmulas geométricas, al considerar las literales como números generales con los que es posible operar. . Sugerencias didácticas Recursos de aprendizaje Incentive a que los alumnos planteen conversiones necesarias para hacer sumas y restas. Antes de hacer el planteamiento pida que hagan cálculos mentales. http://ponce.inter.edu/cremc/ fracciones3.htm Verifique que las construcciones hechas por los alumnos sigan una regla. De no ser así, oriéntelos con preguntas que guíen el análisis de la diferencia o el cociente entre cada par de términos consecutivos de la sucesión. El alumno repasará las similitudes y diferencias entre las sucesiones, de figuras y números, respecto a la progresión aritmética y progresión geométrica. Pídales que analicen cómo se relacionan los términos de una sucesión y que obtenga la regla que define la sucesión. http://www.disfrutalasmate maticas.com/algebra/sucesi ones-series.html Invite a que el alumno describa cómo calcular el perímetro de figuras a partir de un rectángulo. Después, analizará de qué manera se puede expresar el perímetro y el área de triángulos, cuadrados y rectángulos cuando se desconocen sus medidas. Finalmente, estudiará que las fórmulas depende de las caráctersticas de las figuras y no sus medidas. Fórmulas de geometría: http://www.vitutor.net/1/43.h tml © Todos los derechos reservados, Ediciones Castillo. Grupo: Semana 6 Docente: Páginas 51 a 58 6y7 59 a 68 7y8 69 a 72 Ciclo escolar: Eje Forma, espacio y medida. Manejo de la información. Tema Figuras y cuerpos. Escuela: . Lección Contenido Sugerencias didácticas 6. Figuras de tres y cuatro lados. Trazo de triángulos y cuadriláteros mediante el uso del juego de geometría. Haga que el alumno construya triángulos y cuadriláteros. De este modo, podrá analizar algunas similitudes y diferencias entre triángulos equiláteros, isósceles y escalenos, así como entre cuadrados, rectángulos, deltoides, rombos, romboides y trapecios. Sobre el trazado de triángulos y cuadriláteros: 7. Las líneas del triángulo. Trazo y análisis de las propiedades de las alturas, medianas, mediatrices y bisectrices en un triángulo. Propicie que el estudiante repase, mediante su construcción, las rectas notorias de un triángulo: alturas, medianas, mediatrices y bisectrices. Así mismo, que conozca sus propiedades. Incentive que los alumnos hagan trazos libres de triángulos rectángulos, obtusángulos y equiláteros para compararlos entre sí. http://www.vitutor.com/geo/ eso/pl_5.html El alumno tendrá que resolver situaciones en las que usará reparto proporcional. Analizará qué criterios hacen justa repartición, y cuáles no. Escribirá como fracción la proporción que cada parte aportó respecto al total, y la usará a resolver estos problemas. http://www.ditutor.com/prop orcionalidad/repartos_propo rcionales.html Proporcional 8. Reparto idad y proporcional. funciones. Resolución de problemas de reparto proporcional. Recursos de aprendizaje http://www.rena.edu.ve/Terc eraEtapa/dibujoTecnico/traz adodetriangulos.html lñi © Todos los derechos reservados, Ediciones Castillo. Grupo: Semana 8y9 Docente: Páginas 73 a 77 Ciclo escolar: Eje Tema Lección Nociones de 9. Juegos de probabilidad azar. . Escuela: Contenido Identificación y práctica de juegos de azar sencillos y registro de los resultados. Elección de estrategias en función del análisis de resultados posibles. . Sugerencias didácticas Explique la diferencia entre el juego de dardos y el juego se sacar papelitos de una bolsa de plástico. En ambos se obtienen números, pero en el juego de dardos el participante más hábil acertará a los valores más altos, mientras que en el juego de los papeles no importa la habilidad. Recursos de aprendizaje Sobre nociones de probabilidad y ejemplos: http://es.scribd.com/doc/52 184601/Nociones-deProbabilidad-y-Ejemplos © Todos los derechos reservados, Ediciones Castillo.

