Convertidor Boost en Modo Corriente Discontinuo
Anuncio

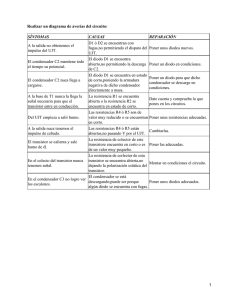
Convertidor Boost en Modo Corriente Discontinuo Una vez analizado el convertidor Boost en modo de corriente continua, el siguiente paso es analizar el mismo circuito pero cuando la corriente entra en modo discontinuo, esto con el fin de obtener los valores críticos de los elementos que pueden establecer una condición de frontera entre los dos estados en que puede estar la corriente sobre la inductancia y demás elementos. Para realizar el análisis del convertidor Boost en modo discontinuo, es necesario dividir los intervalos de tiempo de operación en tres partes de acuerdo a los estados de encendido y apagado de los elementos de conmutación y del ciclo útil a trabajar. Periodo de encendido del transistor entre 0 t DT Durante este periodo, el circuito obtenido es el que se aprecia en la figura 1 [1]. A diferencia del modo continuo, la corriente inicial del inductor en estado estacionario es igual a cero. Figura 1: convertidor en el periodo 0 t DT La tensión a través del inductor y la corriente inicial son iguales a: VL VI L di L , iL (0) 0 dt De lo anterior, se puede obtener que la corriente en el inductor crezca de manera lineal desde 0 hasta un valor máximo obtenido en el tiempo t DT . Despejando la expresión anterior, la corriente a través del inductor, que de acuerdo a la figura 1 es igual a la corriente que circula por el transistor, se expresa como: t i L iS t V 1 1 VL dt VI dt I t L0 L0 L Durante este intervalo. Adicionalmente se ve que la tensión a través del transistor es igual a cero en condiciones ideales, mientras que la corriente que circula por el diodo es cero ya que se encuentra en polarización inversa. También se puede ver que el máximo voltaje en inversa del diodo es igual a VD V0 . La variación de corriente sobre la inductancia es igual al valor pico de la corriente en la misma ya que se inicia desde cero la corriente, por lo que se puede calcular que: i LPico i L i L ( DT ) VI DT L Por su parte, la corriente en el condensador es igual a la corriente de la carga pero en sentido contrario, es decir iC I 0 . Periodo de encendido del diodo entre DT t ( D D1 )T Para este periodo, el transistor es apagado y debido a la corriente sobre el inductor, el diodo es polarizado en directa, lo que lo lleva a un estado de encendido, por ende, la corriente a través del transistor es cero , iS 0 , y la tensión de polarizacion ideal del diodo es cero, VD 0 . El circuito equivalente se muestra en la figura 2 [1]: Figura 2: convertidor en el periodo DT t ( D D1 )T La corriente sobre el inductor comenzara a decrecer linealmente hasta que llegue a un valor de cero, lo cual ocurre en el periodo de tiempo t ( D D1 )T . De igual forma, la tensión sobre el inductor cambia de valor, denotado por: VL VI V0 L di L dt Y como se ve en la figura 2, la corriente sobre el diodo es la misma corriente que atraviesa el inductor, luego el valor de esta corriente a partir de la expresión anterior es igual a: t t (V V0 )(t DT ) 1 1 iL iD VL dt VI V0 dt I L DT L DT L Como la tensión de salida es mayor a la tensión de entrada, y la corriente del inductor es decreciente, la máxima corriente pico sobre estos elementos se calcula a partir de la integral: i LPico i DPico DT DT (V VI ) D1 1 1 VL dt VI V0 dt 0 L ( D D1 )T L ( D D1 )T fS L Donde f S es la frecuencia de conmutación. La tensión sobre el transistor es igual a la tensión de salida, es decir VS V0 , mientras que la corriente sobre el condensador es igual a iC iD I 0 . Periodo de apagado de elementos de conmutación ( D D1 )T t T Durante este periodo, ambos elementos de conmutación (tanto transistor como diodo) se encuentran apagados. El circuito equivalente es el de la figura 3 [1]. En el se ve que la tensión a través del transistor es igual al de la entrada, VS VI , mientras que para el diodo se tiene VD VI V0 . Las corrientes a través del inductor, el diodo y el transistor son iguales a cero. De igual manera, la tensión sobre el inductor es cero. La corriente del condensador es igual a iC I 0 . Figura 3: convertidor en el periodo ( D D1 )T t T Para calcular la función de transferencia del convertidor, miramos la condición sobre el inductor que dice que durante un periodo de conmutación en estado estable, el voltaje promedio debe ser igual a cero, por lo tanto: ___ VL DTVL ( D1 )TVL 0 0 (VI ) DT (VI V0 )(D1 )T V0 D D1 D 1 VI D1 D1 Las ondas de corriente y de tensión ideales de los elementos pueden apreciarse en la figura 4 [1,2]: Figura 4: señales de tensión y corriente en los elementos del convertidor modo discontinuo VI DT ; de acuerdo a la L expresión iC iD I 0 , la corriente promedio del diodo es igual a la de la carga, y con base a la figura 4, la corriente promedio sobre el diodo es igual al área debajo de la curva de corriente de la misma, es decir: La corriente máxima sobre el inductor es igual a i LPico i L I D I0 V0 (VI DT ) D1 RL 2L De donde podemos despejar el valor D1: V 2L D1 0 V I R L DT El valor limite entre modo continuo y discontinuo del convertidor, se obtiene cuando D1 1 D , por lo que reemplazando tenemos que el valor límite para la inductancia para operar en modo discontinuo es: LLIMITE VI RL (1 D) D RL (1 D) 2 D V0 2 f S 2 fS Como era de esperarse, es el mismo límite que tiene el convertidor en modo continuo para calcular su inductor. De igual manera, en base a la figura 4, el cálculo del condensador con ayuda de las áreas rectangulares se facilita, ya que la carga total que almacena es igual a: Q CV0 V0 DT V0 (T ( D D1 )T ) V0T (1 D1 ) V (1 D1 ) C 0 RL RL RL V0 RL f S Donde el valor de tensión del condensador es igual a VC V0 . Procedemos ahora a calcular la corriente RMS del transistor, ya que esta debe ser tenida en cuenta a la hora de calcular la potencia disipada por el mismo. Esto es: iSRMS 1 T DT 0 2 V DT VI t dt I L L D 3 Entonces la potencia absorbida por el transistor es PTransistor (iSRMS )(RDSON ) , donde el transistor es seleccionado en base a una baja resistencia RDSON para que las pérdidas sean bajas. Igualmente la máxima tensión que debe soportar el transistor es igual a VS V0 . El diodo es seleccionado en base al valor de corriente pico igual a (V VI ) D1 V , y en base a una corriente promedio I D I 0 0 , ya que la iDPico 0 RL fS L potencia promedio consumida por el mismo es PDIODO VF I D , donde VF es el voltaje de polarización del diodo, y se escoge uno que tenga un bajo VF para que no consuma potencias grandes que puedan afectar la eficiencia. También, el diodo debe soportar una tensión máxima de polarización inversa igual a VD V0 . Referencias de Bibliografía [1] [2] Marian. K. Kazimierczuk, Pulse-width Modulated DC-DC Power Converters. Dayton, Ohio, USA, Ed. Wiley, 2008, pp. 103–110. Daniel. W. Hart, Electrónica de Potencia. Madrid, Ed. Pearson, 2001, pp. 236–238.