Conferencia 6: Teoria de Produccion
Anuncio

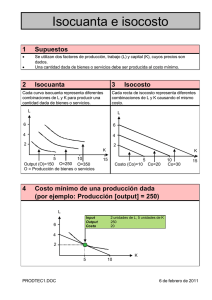
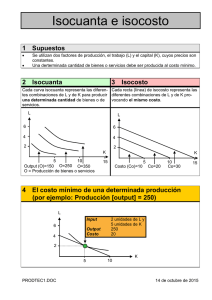
1 UNIVERSIDAD INTERAMERICANA DE PUERTO RICO DEPARTAMENTO DE ADMINISTRACIÓN DE EMPRESAS BADM 4300: Economía Gerencial Prof. J.L.Cotto Conferencia: Teoría y Análisis de Producción Puntos Importantes A. Conceptos Generales • El problema principal que enfrenta una empresa en cuanto a la producción, es determinar cuanto producto producir y cuanta mano de obra y capital emplear para producir la cantidad estipulada en la forma mas eficiente. • Como corolario a lo anterior, el problema es determinar las cantidades optimas de los insumos dado el precio del producto, el(los) precios de los insumos, y la etnología de producción descrita por la función de producción. •. Información de ingeniería en la forma de una función de producción e información económica en la forma de los precios del producto final y los insumos se combinan para contestar la pregunta de cómo producir la cantidad estipulada en forma eficiente. B. La Función de Producción • Todos los insumos o factores de producción se pueden agrupar en dos categorías principales: - Mano de Obra (L) - Capital (K) • La ecuación general para la función de producción es realmente un concepto desprovisto de contenido económico. Esto es, simplemente relaciona el producto Q con con las cantidades de insumos utilizados. Q f(K,L) • Los precios de los insumos (L,K) y del producto (Q) deben utilizarse con la función de producción para determinar cual es la posible mejor combinación de los insumos dados los objetivos de la empresa. • Esta función define la cantidad máxima de producto (Q) que se puede obtener por unidad de tiempo dado una cantidad de mano de obra L y de capital K utilizados. 2 • Los economistas utilizan una variedad de formas para describir la producción. La forma multiplicativa, generalmente conocida como la función de producción Cobb-Douglas: Q AKL es ampliamente utilizada porque tiene propiedades representativas de muchos procesos de producción. • Cuando utilizamos la función podemos ver que una misma cantidad de producto Q se obtiene utilizando distintas combinaciones de mano de obra L y de capital K. A esto se le conoce como “sustitucionabilidad” entre los factores de producción. Este concepto es sumamente importante porque quiere decir que los gerentes pueden cambiar la mezcla de L y K en respuesta a los cambios en los precios relativos de estos. • El problema de la cantidad óptima de producción Q se puede atacar de dos formas: Corto plazo: este es el periodo de tiempo en el cual la cantidad de uno o mas factores estan fijos. Por lo general el capital esta fijo en este periodo. Largo plazo: Se cambian tanto el capital como la mano de obra. Esto implica cambios significativos en la escala de producción. • La relación entre el cambio en el producto total y cambios proporcionales en los insumos se refiere como retorno a escala. Esto quiere decir que si los incrementos en los insumos se duplican, también el producto total se duplicara. • Cuando variamos ambos factores, la función Cobb Douglas produce una serie de productos totales, siendo en algunas ocasiones iguales • En contraste al concepto de retorno a escala, cuando el producto total cambia si uno de los factores aumenta y el otro permanece constante, a esto se le conoce como retorno al factor. • Es importante notar que cuando dejamos uno de los factores constantes (o fijos) el aumento en el producto total ira siendo en incrementos menores. A esto se le conoce como la ley de retornos decrecientes. 3 C. La Producción variando un factor a la vez • Cuando tenemos un proceso de producción con dos variables, el Producto Total de Mano de Obra (TPL), se define como la cantidad máxima que se produce del producto Q, variando la cantidad de mano de obra L, en combinaciones con una cantidad fija de capital K. Expresado en forma de función: __ TPL f (K, L ) • De manera similar el Producto Total de Capital dejando fijo la Mano de Obra expresado en forma de función es: __ TPK f (K, L ) • Dado lo anterior hay dos relaciones del producto importantes; el Producto Marginal de Mano de Obra y el Producto Marginal de Capital: a) Producto Marginal de Mano de Obra MPL, esta se define como el cambio en producto Q, por cambio unitario en mano de obra MPL Q L b) De la misma forma el Producto Marginal de Capital es MPK Q K c) Otro parámetro importante que calculamos bajo el escenario de variar uno de los insumos a la vez es el Producto Promedio (AP) por unidad del insumo que varia y se calcula APL TPL L Producto Promedio de Mano de Obra y APK TPK K Producto promedio de Capital 4 D. El Empleo Optimo de de Uno de los Factores de Producción • En general, para una empresa maximizar la ganancia, debe emplear mano de obra o capital, hasta el punto donde el ingreso adicional (o sea, marginal) asociado al empleo de un unidad extra del factor se igual al costo del empleo (o el precio) de esa unidad extra del factor. MRPL w MRPK r donde W es el precio por unidad de mano de obra donde r es el precio por unidad de capital Este concepto esta dado por La Renta Marginal del Factor • La Renta Marginal que se obtiene al emplear una unidad adicional de L o de K se obtiene MRPL TR MPL xP L y MRPK TR MPK xP K donde P es el precio del producto. E. La producción cuando variamos dos insumos (L, K) • Hasta ahora hemos visto el efecto que tiene en los ingresos el variar uno de los insumos a la vez y el costo de este en cuanto a la toma de decisiones de saber la cantidad máxima de ese insumo que podemos emplear. • Si ahora variamos ambos a la vez ( L,K), la empresa tiene tres formas básicas de determinar las combinaciones optimas de estos recursos: a) maximizar la producción (Q), manteniendo fijo la cantidad total de dólares gastada en L y K. Esto se conoce como La Función de Isocosto. b) minimizar la cantidad gastada de dólares en L y K para una cantidad especifica de producción (Q). Esto se conoce como La Funcion de Isocuanta. c) producir la cantidad Q que maximice las ganancias sin restricciones. • Los primeros dos se conocen como problemas de optimización con restricciones. 5 La Isocuanta de Producción • Aquí variamos L y K de forma tal que siempre obtenemos la misma producción Q y se busca la combinación de L y K que resulte mas costo efectiva (mínima). • El concepto fundamental bajo esta premisa es lo que conocemos como La Tasa Marginal de Sustitución Técnica MRTS, la cual nos indica la tasa a la cual un insumo se puede sustituir por otro para obtener la misma producción Q. MRTS MPL MPK La función describe la tasa de cambio de los insumos en la curva de la Isocuanta. Para calcular el costo mínimo C utilizamos la ecuación C rK wL En este escenario vamos a la matriz de posibilidades de combinaciones de K y L que se obtiene mediante la Funcion Cobbs Douglas, y extraemos las combinaciones de K y L que rinden la misma cantidad Q (de ahí el nombre Isocuanta), y con los precios de capital (r) y mano de obra (W) sustituimos en la ecuación y la combinación de costo C mas bajo, esa será la que nos de la ganancia máxima. La Isocosto de Producción • Si tenemos un presupuesto fijo C podemos calcular cuantos de cada uno podemos comprar y al ir a nuestra función de producción sabremos que cantidad podemos producir con esas restricciones. La Función de Isocosto esta dada por: K C0 w L r r Una vez tengamos las combinaciones de K y L al ir a la matriz producida por la Función Cobbs Douglas, seleccionamos la que maximice Q. Obviamente sabemos que esto nos permite maximizar los ingresos ya que los Ingresos Totales esta dado por TR=P x Q