Nombre: _ Profe(a). Curso

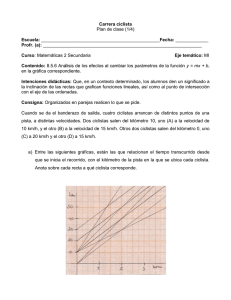
AV. UNIVERSIDAD VERACRUZANA KM. 8 COL. STA. CECILIA C.P. 96537 COATZACOALCOS, VER.
Nombre: ________________________________________________________
Profe(a). Licenciado Isaías Hernández Carrasco
Fecha: ________________
Curso: Matemáticas II
Apartado: 3.8.1
Tema: Representación de la información
Eje temático: MI
Subtema: Gráficas
Conocimientos y habilidades: Analizar el comportamiento de gráficas lineales de la
forma y = mx+b, cuando cambia el valor de m, mientras el valor de b permanece
constante.
Intenciones didácticas:
Que los alumnos analicen el comportamiento de gráficas lineales de la forma y = mx +
b, cuando cambia el valor de m (entero positivo), mientras el valor de b permanece
constante.
Consigna: De manera individual grafiquen en el mismo plano cartesiano las siguientes
funciones con diferentes colores. Posteriormente contesten lo que se pide.
y = x +20
y = 2x + 20
y = 4x + 20
y = 5x + 20
y = 6x + 20
y
x
AV. UNIVERSIDAD VERACRUZANA KM. 8 COL. STA. CECILIA C.P. 96537 COATZACOALCOS, VER.
¿Qué relación hay entre las gráficas y las expresiones algebraicas?
Consideraciones previas:
En caso necesario hay que apoyar a los alumnos en la representación gráfica de las
funciones: tabulación, representación de valores en los ejes, ubicación de puntos en el
plano, etc
Los alumnos, al graficar (dependiendo de las escalas que hayan elegido), encontrarán
gráficas como las siguientes:
y
x
Es conveniente aprovechar la ocasión para mencionar a los alumnos que las gráficas
construidas constituyen una familia de rectas que pasan por un mismo punto. Una recta
está determinada por dos valores (en este caso se habla de la pendiente y la ordenada
al origen), cuando uno de esos valores varía mientras el otro se mantiene constante se
dice que se tiene una familia de rectas.
En este caso, las rectas obtenidas son concurrentes. Tienen en común la ordenada al
origen (20) y varía su pendiente (inclinación).
Es recomendable que el maestro haga la observación de que el tipo de expresiones
algebraicas como las trabajadas anteriormente, pertenecen a la forma general:
y= mx + b, en donde m es la pendiente de la recta y b la ordenada al origen.
AV. UNIVERSIDAD VERACRUZANA KM. 8 COL. STA. CECILIA C.P. 96537 COATZACOALCOS, VER.
Nombre: ________________________________________________________
Profe(a). Licenciado Isaías Hernández Carrasco
Fecha: ________________
Curso: Matemáticas II
Apartado: 3.8.2
Tema: Representación de la información
Eje temático: MI
Subtema: Gráficas
Conocimientos y habilidades: Analizar el comportamiento de gráficas lineales de la
forma y = mx+b, cuando cambia el valor de m, mientras el valor de b permanece
constante.
Intenciones didácticas:
Que los alumnos analicen el comportamiento de gráficas lineales de la forma y = mx +
b, cuando cambia el valor de m (entero), mientras el valor de b permanece constante.
Consigna: De manera individual completen la siguiente tabla, para el caso de la R5
obtengan los datos de su gráfica. Posteriormente grafiquen en el mismo plano las
funciones faltantes y contesten lo que se pide.
Ordenada al
Gráfica
Función
Pendiente
origen
R1
y=x+2
R2
Y = –x + 2
R3
Y = 2x + 2
R4
y = –3x + 2
R5
y
8
7
6
R5
5
4
3
2
1
x
-12 -11 -10 -9
-8
-7
-6
-5
-4
-3
-2
-1
1
-1
-2
-3
-4
-5
-6
-7
-8
2
3
4
5
6
7
8
9
10 11 12 13
AV. UNIVERSIDAD VERACRUZANA KM. 8 COL. STA. CECILIA C.P. 96537 COATZACOALCOS, VER.
¿Qué tienen en común las gráficas construidas?
¿Qué sucede con la gráfica cuando la pendiente es positiva?
¿Qué sucede con la gráfica cuando la pendiente es negativa?
Consideraciones previas:
En caso necesario, apoyar a los alumnos en la representación gráfica de las funciones:
tabulación, representación de valores en los ejes, ubicación de puntos en el plano, etc
En el caso de la expresión algebraica faltante (R5), los alumnos intentarán probando
diferentes expresiones y sustituyendo algunos valores conocidos de “x” e “y” para ver si
se ajustan a ellas. Otros más observarán que en todos los casos la ordenada al origen
es la misma y por lo tanto sólo queda determinar la pendiente, la cual se puede
obtener observando que por cada unidad aumentada en “x” los valores de “y” sólo se
incrementan ½ unidad, así que la expresión buscada es y = ½x + 2. Una forma más
que pudieran usar los alumnos es sustituir en la expresión y = mx + 2, las coordenadas
de un punto de la recta y resolver la ecuación obtenida. Por ejemplo: usando las
coordenadas del punto (2,3) se obtiene la ecuación 3 = m(2) + 2.
Es importante que el maestro aproveche las dudas surgidas en el grupo y las
respuestas dadas por los alumnos para precisar ciertas convenciones relacionadas con
la graficación de puntos en el plano cartesiano: abscisa, ordenada, pendiente,
ordenada al origen, familia de rectas, etc.