Fenómeno de Gibbs
Anuncio

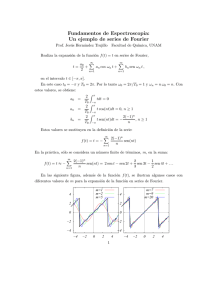
Fenómeno de Gibbs La serie de Fourier en [−1/2, 1/2] de P la función signo f (x) = sgn(x) converge a f pero no uniformemente. Si SN (x) = |n|≤N an e(nx), con an sus coeficientes de Fourier, se tiene lı́m SN (x) = f (x) pero ∀ > 0, lı́m sup SN (x) − f (x) = 00 089 . . . N →∞ N →∞ |x|< Por simetrı́a, el supremos de f (x) − SN (x) tendrá también el mismo valor. En general, uno puede representar un salto de tamaño 2α en una función buena como g(x) + αf (x) con g regular, y este resultado implica que por muchos términos que tomemos en la serie de Fourier no podremos evitar un error por arriba y por abajo como 00 089α, aproximadamente el 9 % de α. A esto se le llama fenómeno de Gibbs. Para probar el resultado anterior se escribe SN (x) = (D ∗ f )(x) con D(t) = X sen((2N + 1)πt) . sen(πt) e(nt) = |n|≤N Usando la definición (D ∗ f )(x) = Z x+1/2 SN (x) = − x R D(y)f (x − y) dy, sen((2N + 1)πt) dt + sen(πt) x Z x−1/2 sen((2N + 1)πt) dt. sen(πt) Cambiando t por −t en la primera integral Z −x SN (x) = − Z x Z + −x−1/2 x = −x x−1/2 Z −x−1/2 + . x−1/2 Cuando x es pequeña, la última integral también lo es. De hecho integrando por partes es posible probar que tiende a cero cuando N → ∞. Por otra parte sen(πt) ∼ πt para |t| pequeño. Como esto se puede probar que Z x sen((2N + 1)πt) dt − f (x) . lı́m sup SN (x) − f (x) = lı́m sup N →∞ |x|< N →∞ |x|< πt −x Dibujando la función h(t) = t−1 sen((2N + 1)πt) es fácil ver su integral entre −algo y algo será máxima cuando algo = 1/(2N + 1), el primer punto donde deja de ser positiva. Entonces el supremo es Z 1/(2N +1) −1/(2N +1) sen((2N + 1)πt) dt − 1 = πt Z 1 −1 sen(πu) du − 1 = 00 08949 . . . πu donde se ha empleado el cambio u = (2N + 1)t, y se ha aproximado la integral con métodos numéricos.