Método tabular - Departamento de Ingeniería Química

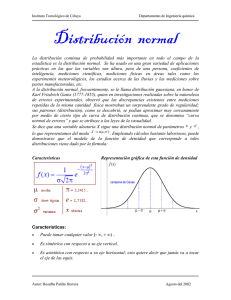
Instituto Tecnológico de Celaya
Datos
Departamento de Ingeniería química
cuantitativos
Cuando la muestra consta de 30 o más datos, lo aconsejable es agrupar los datos en clases y a
partir de estas determinar las características de la muestra y por consiguiente las de la
población de donde fue tomada.
Método tabular
La distribución de frecuencia es la representación estructurada, en forma de tabla, de toda la
información que se ha recogido sobre la variable que se estudia. El primer paso en el método
tabular es el ordenamiento de los datos es decir el acomodamiento de los datos conforme a un
antes y un después. El ordenamiento puede ser ascendente o descendente, conforme los datos
vayan antes de un dato mayor o menor respectivamente
Los datos se acomodan en grupos (clases) conforme a las semejanzas existentes entre ellos.
Antes de hacer la clasificación, es necesario saber cuántos grupos habrá y que datos irán en
cada grupo.
Número de clases (k)
Generalmente no es sencillo manejar más de 20 clases, ni es conveniente
manejar menos de 5, por lo que estos números se establece como límite. Por lo
tanto si se tienen 30 datos (n) serán 6 clases, si 50 datos 10 clases, si 43 datos 9
clases (el número de clases será un número natural), si se tienen 200 datos se
harán 20 clases, etc..
k=
n
5
Intervalo de clase
Es el número de unidades que abarca
cada clase.
Intervalo de clase = Dato mayor- Dato menor
Número de clases
El intervalo de clase también puede variar ligeramente conforme se facilite la clasificación. Así,
si el intervalo de clase resulta 9.6 puede aproximarse a 10, si 0.475 puede aproximarse a 0.5, si
8.8 puede aproximarse a 9 o a 10, aunque al hacerlo cambie el número de clases que también es
arbitrario.
El intervalo de clase obtenido es uniforme para todos los grupos o clases, sin embargo, si se
desea analizar con mayor profundidad una clase determinada, su intervalo de clase puede
dividirse en tantos sub-intervalos como se requiera.
Como regla para un buen análisis se recomienda:
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
(Número de clases)(Intervalo de clases) > Dato mayor - Dato menor
Linderos de clase
Son los puntos de separación entre una clase y otra.
Lindero inferior: es el lindero inferior de cada clase
Lindero superior: es el lindero mayor de cada clase
Con los linderos se presenta una dificultad, ¿dónde clasificar el lindero inferior?, ¿dónde el
lindero superior?. Algunos autores salvan esta dificultad aclarando que a cada clase pertenece
el lindero inferior, pero no el superior. Sin embargo, la mayoría de autores prefiere establecer
un nuevo concepto: límite de clase.
Límite de clase
Son los datos mayor y menor posibles en una clase. Para pasar de linderos de clase a límites de
clase existen tres métodos:
Primer método: Establece una frontera más exacta que los datos. Es decir, si
nuestros datos están dados en enteros nuestras fronteras estarán en decimales, si los
datos en decimales nuestras fronteras en centésimos, si centésimos las fronteras en
milésimos,... Esto puede realizarse de dos formas diferentes: disminuyendo o
aumentando a los linderos media unidad si nuestros datos son enteros, medio décimo
si décimos, medio centésimo,...
Aunque el lindero inferior de la primera clase y superior de la última clase no
representan dificultad alguna de clasificación, la disminución o aumento se realiza
en forma general para mantener el mismo intervalo de clase en todos los grupos.
Segundo método: Consiste en aumentar el lindero inferior de cada clase en una
unidad sí los datos son enteros, en décimos si décimos, en centésimos si
centésimos,...
Tercer método: Se disminuye el lindero superior de cada clase en una unidad si los
datos son enteros, en un décimo si décimos, en un centésimo si centésimos,...
Punto medio de clase ó Marca de clase ( M i )
Es el elemento representativo de los elementos de cada clase y es el punto central del grupo.
Mi =
Límite inf i + Límite supi
2
Frecuencia absoluta (F)
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Es la serie de totales de elementos contenidos en cada clase. Se obtiene mediante el recuento de
datos pertenecientes a cada clase.
Frecuencia relativa (Fr)
Es la serie de porcentajes de elementos contenidos en cada
clase con respecto al total de datos. En cada clase se
obtiene mediante la fórmula:
F ×
Fr =
100
n
Frecuencia acumulada absoluta (Fa)
Es la serie de totales para cada clase de elementos menores al límite inferior de la clase
siguiente (en el ordenamiento descendente serán los totales de elementos mayores al límite
superior de la clase siguiente). Se obtiene de la suma de los elementos de cada clase en cuestión
más los elementos de las clases anteriores.
Frecuencia acumulada relativa (Far)
Es la serie de porcentajes de elementos menores al límite
inferior de la clase siguiente con respecto al total de datos.
Fa ×
100
Far =
n
Ejemplo
Se mide la altura de los niños de la clase de matemáticas y
obtenemos los resultados en cm, haz una tabla de distribución de
frecuencias.
Estatura de 30 alumos:
Número de alumno
1
2
3
4
5
6
7
8
9
10
11
Autor: Rosalba Patiño Herrera
Estatura (cm)
1.25
1.28
1.27
1.21
1.22
1.29
1.30
1.24
1.27
1.29
1.23
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1.26
1.30
1.31
1.28
1.30
1.22
1.25
1.20
1.28
1.21
1.29
1.26
1.22
1.28
1.27
1.26
1.23
1.22
1.21
Si presentamos esta información estructurada obtendríamos la siguiente tabla de frecuencia:
Variable
(valor)
1.20
1.21
1.22
1.23
1.24
1.25
1.26
1.27
1.28
1.29
1.30
Frecuencia
Frecuencia relativa
absoluta
Simple acumulad Simple Acumulada
a
1
1
3.3%
3.3%
4
5
13.3%
16.6%
4
9
13.3%
30%
2
11
6.6%
36.6%
1
12
3.3%
40%
2
14
6.6%
46.6%
3
17
10%
56.6%
3
20
10%
66.6%
4
24
13.3%
80%
3
27
10%
90%
3
30
10%
100%
Si los valores que toma la variable son muy diversos y cada uno de ellos se repite muy pocas
veces, entonces conviene agruparlos por intervalos, ya que de otra manera obtendríamos una
tabla de frecuencia muy extensa que aportaría muy poco valor a efectos de síntesis. (tal como se
verá en la siguiente lección).
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Ejemplo
Supón que medimos la estatura de los habitantes de una colonia y
obtenemos los siguientes resultados (cm
Número de alumno Estatura
1
1.15
2
1.48
3
1.57
4
1.71
5
1.92
6
1.39
7
1.40
8
1.64
9
1.77
10
1.49
11
1.53
12
1.16
13
1.60
14
1.81
15
1.98
16
1.20
17
1.42
18
1.45
19
1.20
20
1.98
21
1.21
22
1.59
23
1.86
24
1.52
25
1.48
26
1.37
27
1.16
28
1.73
29
1.62
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
30
1.01
Si presentáramos esta información en una tabla de frecuencia obtendríamos una tabla de 30
líneas (una para cada valor), cada uno de ellos con una frecuencia absoluta de 1 y con una
frecuencia relativa del 3,3%. Esta tabla nos aportaría escasa información
En lugar de ello, preferimos agrupar los datos por intervalos, con lo que la información queda
más resumida (se pierde, por tanto, algo de información), pero es más manejable e informativa:
Variable
(valor)
1.01-1.10
1.11-1.20
1.21-1.30
1.31-1.40
1.41-1.50
1.51-1.60
1.61-1.70
1.71-1.80
1.81-1.90
1.91-2.00
Frecuencia absoluta
Frecuencia relativa
Simple
1
3
3
2
6
4
3
3
2
3
Simple
3.3%
10%
10%
6.6%
20%
13.3%
10%
10%
6.6%
10%
acumulada
1
4
7
9
15
19
22
25
27
30
Acumulada
3.3%
13.3%
23.3%
30%
50%
63.3%
73.3%
83.3%
90%
100%
El número de tramos en los que se agrupa la información es una decisión que debe tomar el
analista: la regla es que mientras más tramos se utilicen menos información se pierde, pero
puede que menos representativa e informativa sea la tabla.
Método gráfico
Las tablas de frecuencia son sin duda un avance para el análisis de datos, ya que no se requiere
considerar cada uno de los desorganizados datos de la población; sin embargo, conviene
representar en forma gráfica los totales obtenidos en las tablas de frecuencia. Las gráficas
permiten la comparación objetiva de las clases con una sola mirada, a la vez que muestran
rápidamente el avance o retroceso de la frecuencia de una clase respecto a otras.
En las formas que tiene la curva que representa una serie de datos de una muestra podemos
estudiar las siguientes características:
a) Concentración: mide si los valores de la variable están más o menos uniformemente
repartidos a lo largo de la muestra.
b) Asimetría: mide si la curva tiene una forma simétrica, es decir, si respecto al centro de la
misma (centro de simetría) los segmentos de curva que quedan a derecha e izquierda son
similares.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
c) Curtosis: mide si los valores de la distribución están más o menos concentrados alrededor de
los valores medios de la muestra. Se definen 3 tipos de distribuciones según su grado de
curtosis.
Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los
valores centrales de la variable (el mismo que presenta una distribución normal).
Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los
valores centrales de la variable.
Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los
valores centrales de la variable.
Histogramas
Para variables numéricas continuas, tales como la
edad, la tensión arterial o el índice de masa
corporal, el tipo de gráfico más utilizado es el
histograma. Para construir un gráfico de este tipo,
se divide el rango de valores de la variable en
intervalos de igual amplitud, representando sobre
cada intervalo un rectángulo que tiene a este
segmento como base. El criterio para calcular la
altura de cada rectángulo es el de mantener la
proporcionalidad entre las frecuencias absolutas (o
relativas) de los datos en cada intervalo y el área de los rectángulos. Los histogramas de
frecuencias representan un conjunto de datos representan una variable cuantitativa. En el eje
horizontal o de las abscisas se representan los valores tomados por la variable, en el caso de
que los valores considerados sean continuos la forma de representar los valores es mediante
intervalos de un mismo tamaño llamados clases. En el eje vertical se representan los valores de
las frecuencias de los datos. Se puede observar que en un histogramas bajo un proceso en
control, a medida que se crecen las clase tiene aproximadamente la forma de una campana
centrada, que como veremos posteriormente, es la de una de las distribuciones mas importantes
conocidas como frecuencia normal o gaussiana.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
formas que puede tomar un histograma
Ejemplo
La siguiente tabla muestra la distribución de frecuencias de la
edad de 100 pacientes, comprendida entre los 18 y 42 años. Traza
un histograma.
Distribución de frecuencias de la edad en 100
pacientes.
Autor: Rosalba Patiño Herrera
Edad
Número de pacientes
18
1
19
3
20
4
Agosto del 2002
Instituto Tecnológico de Celaya
Autor: Rosalba Patiño Herrera
Departamento de Ingeniería química
21
7
22
5
23
8
24
10
25
8
26
9
27
6
28
6
29
4
30
3
31
4
32
5
33
3
34
2
35
3
36
1
37
2
38
3
39
1
41
1
42
1
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Si se divide este rango en intervalos de dos años, el primer tramo está comprendido entre los 18
y 19 años, entre los que se encuentra el 4/100=4% del total. Por lo tanto, la primera barra
tendrá altura proporcional a 4.
Polígono de frecuencias
Uniendo los puntos medios del extremo superior de las barras del histograma, se obtiene una
imagen que se llama polígono de frecuencias. Dicha figura pretende mostrar, de la forma más
simple, en qué rangos se encuentra la mayor parte de los datos. Un ejemplo, utilizando los datos
anteriores, se presenta en la.
Ejemplo
Con el histograma anterior que muestra la distribución de
frecuencias de la edad de 100 pacientes, comprendida entre los 18
y 42 años. Traza un polígono de frecuencia.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Uniendo los puntos medios del extremo superior de las barras del histogram:
formas que puede tomar un polígono de frecuencia.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Ojiva o Polígono de frecuencias acumuladas:
Una gráfica de distribución de frecuencias acumuladas
es llamada una ojiva. Se trazan los límites reales
superiores contra las frecuencias acumuladas.
Diagramas de cajas
Otro modo habitual, y muy útil, de resumir una variable de tipo numérico es utilizando el
concepto de percentiles, mediante diagramas de cajas. La Figura muestra un gráfico de cajas
correspondiente a la distribución de frecuencias de la edad de 100 pacientes, comprendida entre
los 18 y 42 años. La caja central indica el rango en el que se concentra el 50% central de los
datos. Sus extremos son, por lo tanto, el 1er y 3er cuartil de la distribución. La línea central en
la caja es la mediana. De este modo, si la variable es simétrica, dicha línea se encontrará en el
centro de la caja. Los extremos de los "bigotes" que salen de la caja son los valores que
delimitan el 95% central de los datos, aunque en ocasiones coinciden con los valores extremos
de la distribución. Se suelen también representar aquellas observaciones que caen fuera de este
rango (outliers o valores extremos). Esto resulta especialmente útil para comprobar,
gráficamente, posibles errores en nuestros datos. En general, los diagramas de cajas resultan
más apropiados para representar variables que presenten una gran desviación de la
distribución normal. Como se verá más adelante, resultan además de gran ayuda cuando se
dispone de datos en distintos grupos de sujetos.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Comparación de dos o más grupos.
Cuando se quieren comparar las observaciones tomadas en dos o más grupos de individuos una
vez más el método estadístico a utilizar, así como los gráficos apropiados para visualizar esa
relación, dependen del tipo de variables que estemos manejando.
La comparación de variables continuas en dos o más grupos se realiza habitualmente en
términos de su valor medio, por medio del test t de Student, análisis de la varianza o métodos no
paramétricos equivalentes, y así se ha de reflejar en el tipo de gráfico utilizado. En este caso
resulta muy útil un diagrama de barras de error, como en el ejemplo siguiente:
Ejemplo
Se compara el índice de masa corporal en una muestra de hombres
y mujeres. Para cada grupo, se representa su valor medio, junto
con su 95% intervalo de confianza.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Conviene recordar que el hecho de que dichos intervalos no se solapen, no implica
necesariamente que la diferencia entre ambos grupos pueda ser estadísticamente significativa,
pero sí nos puede servir para valorar la magnitud de la misma. Así mismo, para visualizar este
tipo de asociaciones, pueden utilizarse dos diagramas de cajas, uno para cada grupo. Estos
diagramas son especialmente útiles aquí: no sólo permiten ver si existe o no diferencia entre los
grupos, sino que además nos permiten comprobar la normalidad y la variabilidad de cada una
de las distribuciones. No olvidemos que las hipótesis de normalidad y homocedasticidad son
condiciones necesarias para aplicar algunos de los procedimientos de análisis paramétricos.
Autor: Rosalba Patiño Herrera
Agosto del 2002