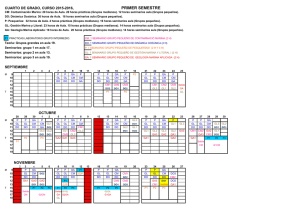
Distribución F - Departamento de Ingeniería Química

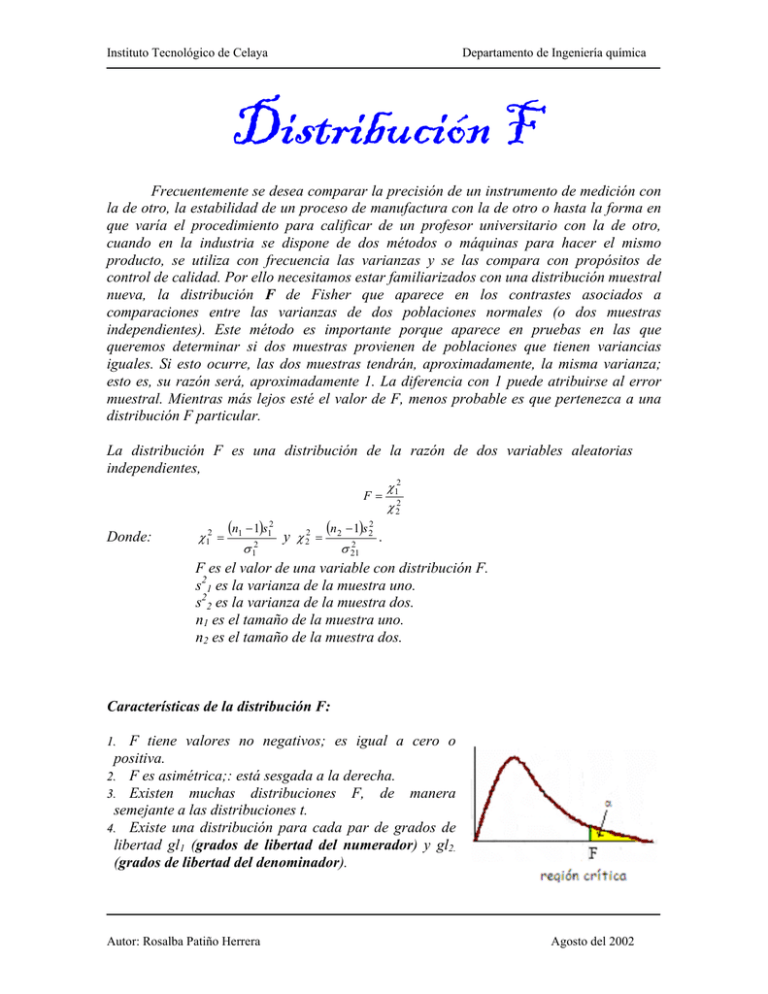
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Distribución F
Frecuentemente se desea comparar la precisión de un instrumento de medición con
la de otro, la estabilidad de un proceso de manufactura con la de otro o hasta la forma en
que varía el procedimiento para calificar de un profesor universitario con la de otro,
cuando en la industria se dispone de dos métodos o máquinas para hacer el mismo
producto, se utiliza con frecuencia las varianzas y se las compara con propósitos de
control de calidad. Por ello necesitamos estar familiarizados con una distribución muestral
nueva, la distribución F de Fisher que aparece en los contrastes asociados a
comparaciones entre las varianzas de dos poblaciones normales (o dos muestras
independientes). Este método es importante porque aparece en pruebas en las que
queremos determinar si dos muestras provienen de poblaciones que tienen variancias
iguales. Si esto ocurre, las dos muestras tendrán, aproximadamente, la misma varianza;
esto es, su razón será, aproximadamente 1. La diferencia con 1 puede atribuirse al error
muestral. Mientras más lejos esté el valor de F, menos probable es que pertenezca a una
distribución F particular.
La distribución F es una distribución de la razón de dos variables aleatorias
independientes,
F=
Donde:
χ 12 =
(n1 − 1)s12
σ 12
y χ 22 =
(n 2 − 1)s 22
2
σ 21
χ 12
χ 22
.
F es el valor de una variable con distribución F.
s21 es la varianza de la muestra uno.
s22 es la varianza de la muestra dos.
n1 es el tamaño de la muestra uno.
n2 es el tamaño de la muestra dos.
Características de la distribución F:
F tiene valores no negativos; es igual a cero o
positiva.
2. F es asimétrica;: está sesgada a la derecha.
3. Existen muchas distribuciones F, de manera
semejante a las distribuciones t.
4. Existe una distribución para cada par de grados de
libertad gl1 (grados de libertad del numerador) y gl2.
(grados de libertad del denominador).
1.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
gl2 = n2 - 1
Para determinar un valor crítico en la tabla F,
localizamos la tabla correcta para α(0.01 o 0.05)
e interceptamos el renglón identificado por
grados de libertad del numerador con la
columna identificada por grados de libertad del
denominador.. Denotaremos la distribución F
por F(n1-1, n2-1).
Grados de libertad para el numerador
.......5
....8
Grados de libertad para el denominador
gl1 = n1 - 1
3.69
Relación entre F y l/F
Si F tiene una distribución en la cual se busca una probabilidad de la cual no tenemos
tablas (extremo izquierdo) se puede recurrir a la siguiente conversión:
F(α −1, gl2 , gl1 ) ) =
1
F(α , gl1 , gl2 )
.
Ejemplo
Se desea conocer F(0.95, 19, 24)= F(0.95,19,24) ) =
Autor: Rosalba Patiño Herrera
1
F(0.05, 24,19 )
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Ejemplo
Encuentra el valor de F, si el área a la derecha de F, es de 0.25 con
gl1=4 y gl2=9.
Como el área que da la tabla es de cero a Fisher, se tiene que localizar primero los grados
de libertad dos que son 9, luego un área de 0.75 con 4 grados de libertad uno.
Ejemplo
Encuentra el valor de F, si el área a la izquierda de F, es de 0.95 con
gl1=15 y gl2=10.
En este caso se puede buscar el área de 0.95 directamente en la tabla con sus respectivos
grados de libertad.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Departamento de Ingeniería química
Ejemplo
Encuentra el valor de F, si el área a la derecha de F es de 0.95 con
gl1=6 y gl2=8.
Se tiene que buscar en la tabla un área de 0.05, puesto que nos piden un área a la derecha
de F de 0.95.
Ejemplo
Encuentra el valor de F, si el área a la izquierda de F, es de 0.10 con
gl1=24 y gl2=24
Se busca directamente el área de 0.10, con sus respectivos grados de libertad.
Autor: Rosalba Patiño Herrera
Agosto del 2002
Instituto Tecnológico de Celaya
Autor: Rosalba Patiño Herrera
Departamento de Ingeniería química
Agosto del 2002