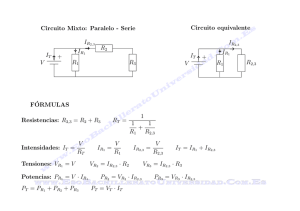
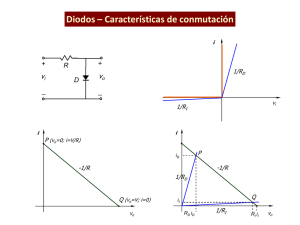
Vp = 0,7 + Vk Vcc
Anuncio

1 VC C 4k Vth = 15 · 20k = 12 5k + 20k Rth = 5k · 20k = 4k 5k + 20k 5k 10k Q1 PN P PUT 20k 2 0k C 1uF 50 Rk Vcc = 4k · ie + 0,7 + Rth ib + Vth VCC 4k ie Q1 PNP ib Vth Vcc = 4k (β + 1) · ib + 0,7 + Rth ib + Vth Rth ic C 1uF ib = 15 − 12 − 0,7 = 2,846µA 4k · 201 + 4k ic = βib = 0,569mA T Vp Vc Vc = ic t + Vv C Vv t2 t1 Vp-Vv Vc (t = t1 ) = Vp VRK t1 = 10 · 1µf (Vp − Vv ) C = = 17,574ms ic 0,569mA Figura 1. Gráficas de la pregunta 1 t2 = Rk C · ln Vp = 0,7 + Vk Vk = Vcc · 20k = 10 10k + 20k Vp = 10,7 Vp Vv = 50 · 1µf · ln 10,7 0,7 T = t1 + t2 = 17,71ms = 0,136ms 2 VF = 100 sin(wt) f = 60Hz Pregunta 2. R1 = 1k R2 = 2k π 3π α1 = α2 = 4 2 x1 = arcsin VF p 0 −30 100 R3 = 1k E = 30 = −0,3 = −17,45◦ 2p x2 = π − x1 = 3,446 = 197,45◦ Vg a2 a1 x3 = 2π + x1 = 5,97 = 342,54◦ π ≤ wt ≤ x2 4 100 sin (wt) + 30 VR1 = VR3 = 2 VR2 = 0 VF+E x3 x2 x1 3π ≤ wt ≤ x3 2 2 (100 sin (wt) + 30) VR2 = 3 100 sin (wt) + 30 VR3 = 3 VR1 = 0 VR1 a1 x2 VR2 a2 x3 " Vdc (R3 ) = Vdc (R3 ) = VR3 a2 a1 1 2π 1 2π ´x2 (100 sin(wt)+30) π 4 2 dwt + ´x3 3π 2 # (100 sin(wt)+30) dwt 3 h x 50 − cos(wt) π2 + 15 x2 − π4 · · · 4 x3 x · · · + 100 − cos(wt) 3π3 + 10 x3 − 3 x2 2 Vdc (R3 ) = Figura 2. Gráficas de la pregunta 2 1 2π [83,055 + 39,912 − 31,8 + 12,66] Vdc (R3 ) = 16,5245 3π 2 i 3 T1 R1 Vf VF π 0 L1 π √ VF = 220 2 sin(wt) f = 60Hz R1 = 1Ω L1 = 2,65mH π 3π α= y α= 3 2 Vg 2 1 XL = wL = 2πf L = 2π · 60 · 2,65mH = 1 q Z = R2 + XL2 = 1,4142 XL φ = arctan = 0,7853 = 45◦ R IRL 2 1 β2 β1 α= π 3 α= y π 2 φ= y π =⇒ β1 = 3,9122 = 224,15◦ 4 φ= β2 = π + β VRL β1 β2 √ 2 = Vrms (220 2) 2 (220 2) 2 ··· β2 √ 2 Vrms = (220 ´β1 2 sin (wt)dwt + π 3 2π IT1 2 " 2π √ 2 = Vrms β1 =⇒ β2 = 6,9965 = 400,87◦ 2 1 1 π =⇒ β = 3,855 = 220,87◦ 4 2) 2π h 3π β1 +β2 − π 3− 2 2 Vrms = 187,96 1 β1 β2-2π Figura 3. Gráficas de la pregunta 3 2 # 2 sin (wt)dwt 3π 2 ··· 3π sin(2 π 3 )+sin(2 2 )−sin(2β1 )−sin(2β2 ) + 4 2 [2,574 − 0,2807] √ q 2,2933 Vrms = 220 2 2π VAK1 ´β2