cap 07 Resalto Hidráulico
Anuncio

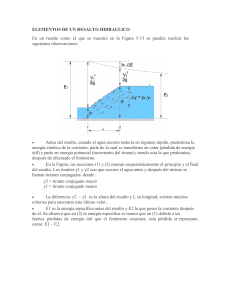
________________________________________________Capitulo 7.Resalto hidráulico CAPITULO 7. EL RESALTO HIDRÁULICO 1 INTRODUCCIÓN. En el Capítulo 2 se describió el resalto hidráulico como resultado de igualar las fuerzas específicas a lado y lado de la discontinuidad que aparece en el flujo. Esta ecuación viene dada por la expresión de Belanger para canal rectangular y por una expresión más compleja en el caso de que el canal sea más irregular. Ambas expresiones se expresan nuevamente a continuación. La expresión general: gy1A1 + Q 2 / A1 = gy2A2 + Q 2 / A2 (7.1) y la fórmula de Belanger para canal rectangular como: y1 1 = (−1 + 1 + 8Fr2 ) y2 2 (7.2) La aplicación de la ecuación (7.2) es muy fácil, simplemente conociendo la situación a un lado de la discontinuidad el otro lado queda explícito inmediatamente. En el caso de usar la ecuación (7.1) el problema deberá realizarse mediante una estimación iterativa, por ejemplo utilizando el método de Newton de aproximaciones sucesivas para funciones no lineales. Esto mismo hace el programa HecRAS puesto que los cauces suelen ser sistemas complejos, incluso como vimos con varios mínimos en la energía y por supuesto también en la ecuación de momento. 2 EJEMPLO DE CÁLCULO. Un canal tiene un calado de 0.2 m donde se presenta una discontinuidad, dado que la anchura del mismo es de 1m y la velocidad de 2.5 m/s, evalúe el calado conjugado y las características del flujo. Así los cálculos quedan como se muestra a continuación: 2 q = v1y1 = 1 × 0.2 = 0.2 m s q2 = 0.16m yc = g α1 = 1.25 3 2 Fr1 = q 2 gy13 = (0.2) (9.81 × (0.2) ) 3 = 0.71 régimen lento 1 ________________________________________________Capitulo 7.Resalto hidráulico Aplicando Belanger y1 0.2 −1 + 1 + 8Fr12 = −1 + 1 + 8 × 0.712 = 0.12 m 2 2 El Froude del régimen rápido será: y2 = ( ) 2 Fr2 = q gy2 3 ( ) = 1.53 La pérdida de carga en el resalto desde aguas arriba (régimen rápido) hacia aguas abajo (régimen lento), será: 3 DH = (y1 − y2 ) 4y1y2 = (0.2 − 0.12)3 = 0.005 m 4 × 0.2 × 0.12 Ahora bien cuando la sección es diferente a la rectangular el cálculo es más complejo y la forma de abordarlo es mediante el uso de métodos numéricos. Al final de este apartado encontrará una tabla con las relaciones geométricas para otro tipo de secciones. El caso anterior se puede resolver mediante el uso del Hec-Ras y por tanto pierde importancia, hay otras condiciones en las que el HecRas no puede resolver el problema y es cuando la pendiente del régimen rápido, es elevada. Las pendientes elevadas suelen ser de más del 10%, por que en este caso la cantidad de movimiento del flujo va en una dirección muy diferente a las condiciones de canal de pequeña pendiente. En este caso existe el desarrollo de un ecuación semi empírica estudiada y formulada por Kindsvater (1944) sobre datos y anotaciones de Yarnell después de su muerte, que se expresa de la siguiente forma: cos3 θ y2 1 = −1 + 1 + 8Fr 2 1 − 2N tan θ y1 2 (7.3) En donde N es un factor empírico relacionado con la longitud del salto. Si se define a cos3 θ Γ = 1 − 2N tan θ (7.4) G12 = Γ12Fr12 (7.5) 2 1 entonces, 2 ________________________________________________Capitulo 7.Resalto hidráulico y la ecuación (7.3) queda reducida a la siguiente expresión: y2 1 = −1 + 1 + 8G12 y1 2 (7.6) En el caso de tener este tipo de problemas es conveniente tratar de resolver el problema manualmente y no mediante el Hec-Ras. En este caso se deberá consultar adecuadamente un libro de Hidráulica y se puede proceder de forma acoplada con el Hec-Ras realizando una introducción de la información mediante condiciones de contorno impuestas. Rajaratnam (1967) expresa la siguiente relación: Γ1 = 100.027 θ (7.7) el ángulo θ se da en grados. 3 EJEMPLO : LOCALIZACIÓN DE UN RESALTO. En un canal rectangular de 10 metros de anchura y alta pendiente 5%, circula un caudal de 30 m3/s. El coeficiente de Manning es de 0.016. La longitud total del canal es de 20 m y la entrada se da en régimen crítico y la condición de contorno aguas abajo es un calado de 2 m. q = Q B = 3m 2 / s yc = 3 q2 = 0.97m g 2 n 2Q 2 Sc = = 0.032 A2R 4 3 Se realiza el cálculo del régimen rápido mediante el método paso a paso, partiendo del calado crítico. Se obtiene la gráfica de la Figura 1 3 ________________________________________________Capitulo 7.Resalto hidráulico Resalto Hidráulico 101.5 20 18 101.0 16 Lámina Cota fondo 14 3 Fuerza Específica 12 Cotas (m) Fuerza específica (m ) 100.5 100.0 10 8 99.5 6 4 99.0 (Resalto) 2 98.5 0.00 5.00 10.00 15.00 0 25.00 20.00 Distancia (m) Figura 1. Curva de remanso S2. Se muestra también la fuerza específica de la curva. 30 101.0 25 100.5 20 100.0 15 99.5 10 99.0 3 101.5 Fuerza específica (m) Cotas (m) Resalto Hidráulico 5 (Resalto) 98.5 0.00 5.00 10.00 15.00 20.00 0 25.00 Distancia (m) Figura 2. La solución del régimen lento. Se valora el calado conjugado del nivel de agua a la salida del canal, esto es justo donde se da la condición de contorno. En esta sección el calado es 0.53 m y el número de Froude es 2.50. Así aplicando Belanger por ser canal rectangular se obtiene: y* = yr 0.53 −1 + 1 + 8Frr 2 = −1 + 1 + 8 × 2.52 = 1.62m 2 2 ( ) ( ) (7.8) El conjugado es 1.62m que resulta ser menor que el calado del contorno 2. Es decir la fuerza especifica del calado de 1.62 es menor que la fuerza específica del calado de 2m, por lo 4 ________________________________________________Capitulo 7.Resalto hidráulico que domina el contorno y entra en el canal un resalto hidráulico que se extenderá hacia aguas arriba hasta que se compense con el flujo rápido y se estabilice. Por tanto la solución pasa por evaluar la curva de remanso lenta, partiendo desde el contorno con un calado de 2m. Esta solución se presenta junto con la evaluación de la fuerza específica en la . En esta solución cuando el calculo se extiende hasta la arriba, cada vez se tiene menos energía específica, hasta que se llega al mínimo y por debajo del mínimo. Ya no se puede transportar el caudal de agua en estas condiciones y la solución no existe, se ha decidido como lo hace el Hec-Ras de colocar el valor del calado crítico. La solución se encuentra superponiendo las dos gráficas y escoger como solución buena el calado que tiene más fuerza específica de las dos soluciones. Este proceso es sencillo pero ha requerido el cálculo de la fuerza específica con antelación. La Figura 3 muestra este procedimiento. 30 101.0 25 100.5 20 100.0 15 99.5 10 99.0 3 101.5 Fuerza específica (m ) Cotas (m) Resalto Hidráulico 5 (Resalto) 98.5 0.00 5.00 10.00 15.00 20.00 0 25.00 Distancia (m) Figura 3. El resalto se da en el cruce de las curvas de fuerza específica para ambos cálculos. El resultado final es el que se muestra en la Figura 4 5 ________________________________________________Capitulo 7.Resalto hidráulico Lámina Resalto Hidráulico Cota fondo 101.5 Cotas (m) 101.0 100.5 100.0 99.5 99.0 98.5 0.00 5.00 10.00 15.00 20.00 25.00 Distancia (m) Figura 4. Resultado final del cálculo de la curva de remanso y situación del resalto hidráulico. 6 ________________________________________________Capitulo 7.Resalto hidráulico 7