Modelo de los potenciales electroquímicos
Anuncio

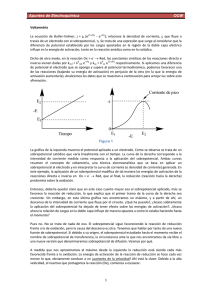
Modelo de los potenciales electroquímicos. i i , para especies sin carga. i io RT ln ai ( io es el potencial químico estándar y ai la actividad de la especie i en la fase ). Como sabemos, el potencial químico en una fase , i , se puede definir, para el caso de una reacción química en general, como actividad es unitaria. G i ni T ,P ,n (32) Sin embargo, para el caso de una reacción electroquímica resulta conveniente introducir el concepto de potencial electroquímico, i , cuya diferencia con el potencial químico es que, éste último incluye el efecto de un campo eléctrico(que produce una migración iónica), de manera que se puede definir como G i ni T ,P ,n e eo , para electrones en un metal(la concentración de e no cambia apreciablemente). k i donde ni es elnúmero de moles de la especie i en la fase . i io , cuando la fase es pura y la Cuando existe equilibrio entre dos fases y , para la especie i: i i . Para la reacción, general k O ne R z2 z1 en donde z2 – z1 = - n, las constantes de (33) k i (35) k equilibrio k y k , vienen dadas por la ec. de Arrhenius: donde i es el potencial electroquímico para la especie i en la fase y G es la energía libre electroquímica. La separación de las dos componentes (química y eléctrica), es sólo un artificio matemático conveniente, pero en la realidad, no es posible separarlos experimentalmente. El potencial químico y el electroquímico estan relacionados por la siguiente ecuación i i zi F (34) en ella, zi es la carga de la especie i y F, representa el efecto eléctrico local, a una escala mayor que la de cualquier carga iónica. Ahora bien, para aplicar el modelo de los potenciales electroquímicos, será conveniente listar las propiedades del potencial electroquímico: Fig. 1 Separación del potencial electroquímico en sus componentes químico y eléctrico. kT k e h kT k e h G RT (36) G1o O ne OoS z1F S neoM nF M (42) G RT (37) en donde G y G , son las energías libres electroquímicas de activación, que se pueden separar en las componentes química y eléctrica: e e G G G (38) de igual forma, para el lado derecho de la reacción, R z2 , podemos escribir G2o R RoS z2F M (43) luego, la componente eléctrica (Go)e, es la diferencia entre las partes eléctricas correspondientes de reactivos y productos, es decir y G G G (39) e y G e G o (40) e 1 G o o e luego, de acuerdo con el esquema de la Fig. 5, si el componente eléctrico es considerado unitario, cada componente eléctrico en un sentido y en otro de la reacción, representará una fracción de dicha energía (siendo los dos mutuamente complementarios), es decir G G e (41) lo que significa que las energías de activación( G hacia la derecha o hacia la izquierda), no cambian con el potencial, y que éste último se manifiesta totalmente en las componentes eléctricas. Ahora bien, para el lado izquierdo de la z reacción (35), O 1 ne , de acuerdo con la definición de potencial electroquímico y sus propiedades, se puede escribir para la energía libre electroquímica molar, G1o , z2F S z1F S nF M z2 z1 F S nF M pero (z2 – z1) = – n, por tanto G o e nF M S (44) Ahora, dado que el potencial de electrodo, E, contra un sistema de referencia cualquiera, está relacionado con el potencial interfacial, M – S, por una constante, , podemos escribir E M S por tanto G o e luego, nF E (45) G e G e nF E 46) 1 nF E (47) Substituyendo (46) y (47) en (38) y (39), respectivamente, tenemos G G nF E (48) y G G 1 nF E (49) reemplazando ahora en (36) y (37), se tiene k k kT G / RT nF / RT nFE / RT (50) e e e h kT G / RT 1 nF / RT e e h velocidad respectivas( k 0 y k 0 ) a E = 0, o sea kT G / RT nF / RT k0 e e h k k 0 e 1 nFE / RT (55) que son precisamente las ecuaciones (27) y (28), encontradas anteriormente en el caso del modelo de las curvas de energía libre. A partir de ellas, como antes, se puede llegar a la expresión para la corriente, ec. (31). Condiciones de equilibrio. En el equilibrio, para un proceso electródico, la corriente neta es igual a cero, por tanto se requiere que el electrodo adopte un potencial que dependerá de las concentraciones masivas de O y R, como lo establece la ec. de Nernst. A corriente cero, entonces, tenemos [ec. (31)] nFk oCO,S e nF Eeq E o / RT 1 nF Eeq E o / RT (56) kT G / RT 1 nF / RT e e h en tal caso, las concentraciones en la superficie del electrodo, CO,S y CR,S, se igualan con las concentraciones masivas, CO* y CR* , tomando E su valor de equilibrio, Eeq, luego 1 nF E luego (54) (51) en estas ecuaciones, los primeros dos factores son independientes del potencial y pueden ser igualadas a las constantes de k0 nFk oCR ,S e e 1 nFE / RT k k 0 e nFE / RT (52) E o / RT eq CO* e nF Eeq E o / RT CR* e (53) o CO* nF Eeq E o / RT e CR* (57) y, tomando logaritmos, ln CO* nF E eq E o / RT * CR (58) E eq CO* 2.303RT E log * nF CR CO* * CR C C (59) * R * o también o nF Eeq E o / RT (61) Por otro lado, elevando a la - ámbos miembros de la ecuación(57), podemos escribir Desarrollando ahora la última expresión y cambiando a logaritmo de Briggs, nos queda CO* 2.303RT log * Eeq E o nF CR j o j j nFk oCO* e e e nF Eeq E o / RT C * R* CO nF Eeq E o / RT O Reemplazando la exponencial en la ec. (61), tenemos (60) como puede apreciarse, la ecuación anterior es precisamente una de las formas de la ec. de Nernst. Por ello, cualquiera de los dos modelos(energías libres o potenciales electroquímicos), soportan una de las pruebas de la realidad, es decir, generar la ec. de Nernst para las condiciones de equilibrio. C j j nFk C nFk C C jo jo o o * 1 O CO* * R * R * O (62) (63) Relación corriente-sobrepotencial. Corriente de intercambio. Sobrepotencial. Si hacemos ahora la consideración de que existe, a corriente cero, cierta actividad farádica balanceada (es decir, que i i ), entonces ámbas corrientes (en un sentido y en otro) podrían expresarse en términos de la corriente de intercambio io, (en magnitud: La polarización de un electrodo, , se define como la diferencia entre su potencial de operación(o a la corriente i, i) y su potencial de equilibrio, eq, es decir: i o i i ). Lo anterior, también es válido = i - eq (64) para la corriente normalizada ( j o j j ). Pero, como en el equilibrio CO,S CO yE= Eeq, de (31) tenemos y, cuando el potencial eq no corresponde al potencial de equilibrio sino al potencial estacionario, est(que puede mantenerse por un periodo proplongado), tenemos = i - est (65) Luego, dado que el potencial es desplazado hacia el lado negativo cuando se imprime una corriente catódica y hacia el lado positivo cuando se imprime una anódica, la polarización catódica será siempre negativa y la anódica positiva. polarización catódica: i eq 0 i est 0 polarización anódica: i eq 0 i est 0 En general, todo proceso electroquímico es influido por la velocidad con que se desarrollan los siguientes pasos de reacción: 1. Transferencia de masa y carga eléctrica desde el seno de la solución hacia la interfase metal/solución. 2. Transferencia electrónica a través de la interfase. 3. Reacción química que precede o sigue a la transferencia electrónica. Puede ser un proceso homogéneo o heterogéneo. 4. Otras reacciones de superficie: adsorción, desorción o cristalización (electrodepósito). De acuerdo con lo anterior, es posible clasificar el fenómeno de polarización, dependiendo de cual sea el paso que controle la reacción global de electrodo. Para el caso, el término sobrepotencial (), se usa en vez de polarización, cuando el paso limitante de una reacción es conocido. Se llama polarización por concentración(c) a la que se da como consecuencia de un retardo en el transporte iónico y los pasos de transformación química; cuando todos los pasos de un proceso de electrodo son reversibles a excepción del transporte de reactivos, se dice que hay un sobrepotencial de difusión(d); si todos los pasos de la reacción, a diferencia de la transformación química, proceden reversiblemente, entonces la polarización se denomina sobrepotencial de reacción(r); existe un sobrepotencial por transferencia electrónica(e) cuando el paso de transferencia electrónica es retardado; por último, cuando se da una incorporación o separación de iones metálicos en el electrodo, se dice que hay un sobrepotencial de fase(f). El sobrepotencial global, , agrupa los sobrepotenciales de concentración y activación(o transferencia electrónica). En general, la desviación real entre el potencial de equilibrio y el de operación es el resultado de la superposición de todos los tipos de sobrepotencial.