Unidad de indUctancia BoBinas de indUctancia
Anuncio

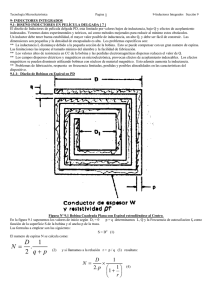
24 electricidad Inducción electromagnética Entrega 3 Autor: Ing. José Barona Gurrea Unidad de inductancia Cuando se origina un voltaje inducido de 1 V al producirse una variación de 1 A, en un segundo, en la corriente que atraviesa una bobina, se dice que la inductancia de ésta es de 1 Henrio. El nombre de esta unidad es un homenaje al experimentador estadounidense Joseph Henry, cuyos descubrimientos sobre electromagnetismo fueron simultáneos con los de Faraday. En las aplicaciones prácticas, especialmente en la radio se utilizan inductancias de valores muchísimo menores que el henrio, empleándose como unidades convencionales el mili henrio, que es la milésima parte del Henrio y el microhenrio equivalente a la millonésima parte de esta unidad. Las representaciones abreviadas de estas unidades son: H= Henrio; mH = milihenrio y μH= microhenrio. Bobinas de inductancia Las bobinas utilizadas en la radio son de valores muy diferentes que varían entre microhenrios y hasta 100 henrios. Es muy frecuente el empleo de 1 1 Bobina 3 a b 4 + En los manuales figuran una serie de fórmulas más menos complicadas para calcular la inductancia de una bobina en función de sus características, de las que vamos a indicar las más usuales. Bobina cilíndrica de una sola capa de espiras (figura 10 a) 2 R las del orden de los 300 μH que tienen un diámetro que varía entre 0,5 y 3 cm y están formadas por 50 a 100 espiras de hilo de 0,2 a 0,3 mm de diámetro, con aislamiento de esmalte, seda o algodón. I 2 Núcleo de hierro 3 Lámpara 4 Batería - Si N es el número de espiras de la bobina, a) su radio, y b) su longitud. La inductancia de la bobina, con núcleo de aire será: Figura 9. Experiencia demostrativa de la ley de Lenz. Al interrumpir el circuito, luce la lámpara para cuyo encendido resultaba insuficiente el voltaje V de la batería ELECTROSECTOR | Agosto 2016 L= 0,394 a2 N2 µH 9a + 10b (1) 26 electricidad y expresando, como siempre, las dimensiones en cm, tendremos: b b 1º= Para la bobina con núcleo de aire: c a a L= 0,315 x 1,752 x 12002 = 1440000 6 x 1,75 + 9 x2 + 10 x 1,5 43 = 33,490 µH (aproximadamente) = 33,49 mH 2º= Para la bobina con núcleo de hierro: L =33,49 mH x 3000 = 100 H A (aproximadamente). B Inductancia mutua Figura 10. Corte transversal de bobinas cilíndricas. (a) De una sola capa de espiras. (b) De varias capas de espiras Si tuviese núcleo magnético el valor obtenido habría que multiplicarlo por el coeficiente de permeabilidad del núcleo. La inductancia de la bobina, con núcleo de aire, será: Ejemplo: ¿Cuál será la inductancia de 6a + 9b + 10 una bobina de una sola capa, formada por 300 espiras de hilo de 0,5 mm, devanadas sobre una forma cilíndrica de 15 cm de longitud y 4 cm de diámetro? Aplicando la fórmula (1) y expresando los valores de las longitudes en cm tendremos: 2 2 L= 0,394 x 2 x 300 = 141840 = 844 µH 9 x 2 + 10 x1b 168 Bobinas cilíndricas con varias capas de espiras (figura 10 b) Siendo N el número de espiras a) el radio medio de la bobina b) su longitud y c) su altura. 2 2 L= 0,315 a N µH (2) Ejemplo: ¿Cuál será la inductancia de una bobina de 1200 espiras de hilo de 0,5 mm de diámetro devanadas en 30 capas de espiras sobre una forma de baquelita de 20 mm de diámetro: 1º con núcleo de aire; 2º con núcleo de hierro de permeabilidad 3000? Siendo 20 mm el diámetro de la forma sobre la que va devanada la bobina, su altura c = 15 mm y su longitud b = 20 mm, el radio medio a será: 20 c + = 17,5 mm. 2 2 Llevando a la fórmula (2) los valores correspondientes a este caso ELECTROSECTOR | Agosto 2016 Refiriéndonos nuevamente al caso representado en la figura 7 en la que tenemos dos bobinas, P y S, próximas, se dice que están acopladas magnéticamente y este acoplamiento será tanto mayor, cuanto mayor sea el número de líneas de fuerza del campo creado por la corriente que circula en el primario porque atraviesa las espiras del secundario, S. De acuerdo con el valor de este acoplamiento se dice que es “fuerte” o “débil”. Es evidente que aumentará el acoplamiento cuanto mayor sea la permeabilidad del medio atravesado por las líneas de fuerza y cuanto más próximas estén las bobinas. El voltaje desarrollado en la bobina S dependerá de las dimensiones de las bobinas, de su separación, de la permeabilidad del medio y de la rapidez con que varíe la in-