Distribuciones Continuas - Centro de Ciencias de la Atmósfera, UNAM
Anuncio

Distribuciones continuas
• Si aumenta indefinidamente el número de
observaciones y la amplitud de clase tiende
a cero, el histograma, al igual que el
polígono de frecuencias, se acerca a la
forma de una curva continua.
• Si la altura de la curva de frecuencias fuera
estandarizada de manera que el área bajo
dicha curva fuera igual a la unidad,
entonces se determinaría una distribución
probabilística continua.
• Los cálculos de probabilidades para v.a.
continuas involucran la integración de
funciones continuas llamadas Funciones
de Densidad de Probabilidad (PDF), f(x).
• La integral de cualquier PDF sobre todos
los valores posibles de x debe ser igual a 1:
, fX(x) ≥ 0 para toda x
Los límites de integración dependen de la PDF en cuestión.
La probabilidad es proporcional al área bajo la curva de la PDF y no a la
altura.
La probabilidad de observar un valor específico de la v.a. X, como x = a,
es nula ya que la integral sería cero.
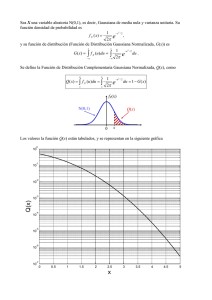
La función de distribución acumulativa (CDF), especifica la
probabilidad de que la v.a. X no exceda de un valor particular, x:
F(-∞) = 0, F(∞) = 1
x2
Pr{x1 < X < x2} = ∫x1f(x)dx = F(x2) - F(x1)
La integral se calcula a partir del valor mínimo que puede tomar X
hasta el valor particular x de interés.
Como los valores de F(x) son probabilidades, 0 ≤ F(x) ≤ 1.
f(x) se puede calcular como la derivada de F(x) en los puntos donde
exista.
Valores esperados para variables continuas
Distribución Uniforme
•
La v.a. X puede tomar cualquier valor entre dos números a y b,
sin favorecer ninguna zona del intervalo [a,b].
Distribución Gaussiana o Normal
• La distribución Gaussiana juega un papel central en la estadística clásica
y tiene muchas aplicaciones en las ciencias atmosféricas. Su PDF es la
curva en forma de campana y se expresa como sigue:
• Los dos parámetros de la distribución son la media, µ, y la desviación
estándar, σ.
Aproximadamente el 68% de todos
los valores de una población con
distribución Gaussiana se encuentra
dentro del intervalo (µ-σ, µ+σ).
Aproximadamente el 96% de todos
los valores de una población con
distribución Gaussiana se encuentra
dentro de (µ-2σ, µ+2σ).
Casi toda la probabilidad se
encuentra dentro del intervalo µ±3σ.
Los valores de µ y de σ se estiman a
partir de los estadísticos muestrales
x y s, una vez que se ha determinado
que los datos de la muestra siguen
aproximadamente una distribución
normal.
¿Cómo calcular las probabilidades para una distribución Gaussiana?
• La integración analítica de la PDF Gaussiana es imposible de modo que no se
puede obtener una fórmula para la CDF, F(x), correspondiente.
• Las probabilidades se calculan mediante integración numérica o utilizando
valores tabulados.
• Generalmente se requiere realizar una transformación a los datos ya que las
tablas proporcionan los valores de la distribución Gaussiana estándar (ϕ(z)),
e.d., con µ = 0 y σ = 1.
Ejercicios:
1.
Suponiendo que las temperaturas promedio mensuales para Enero en
Ithaca están bien representadas mediante una distribución Gaussiana con
μ = 22.2°F y σ = 4.4°F. ¿Cuál es la probabilidad de que en un Enero
elegido arbitrariamente, o en un Enero futuro, la temperatura promedio
sea menor o igual a 21.4°F?
2.
¿Cuál es la temperatura promedio de Enero en Ithaca para la cual z =
0.18?
3.
¿Cuál es la probabilidad de que la temperatura promedio de Enero en
Ithaca no sea mayor a la obtenida en la pregunta anterior?
4.
Calcular la probabilidad de que la temperatura promedio de Enero en
Ithaca esté entre 20°F y 25°F.
5.
Encuentra la temperatura promedio de Enero en Ithaca que definiría al
10% de los Eneros más fríos (e.d., el decil inferior).
6. Un profesor de un grupo numeroso de estudiantes los califica
de la siguiente manera:
a. Si la puntuación es mayor que x + 1.6s, la calificación es A
b. Si x + 0.4s <= puntuación <= x + 1.6s, la calificación es B
c. Si x – 0.4s <= puntuación < x + 0.4s, la calificación es C
d. Si x – 1.6s <= puntuación < x – 0.4s, la calificación es D
e. Si la puntuación es menor que x – 1.6s, la calificación es F
Suponiendo que las puntuaciones están distribuidas de manera
normal con una media x y una desviación estándar s, ¿cuál es
el porcentaje de cada calificación otorgada por el profesor?
• Distribución Normal Bivariada: La probabilidad corresponde geométricamente al
volumen bajo la superficie definida por la PDF:
Una propiedad muy útil de esta distribución es que la distribución condicional de una
de las variables, dado un valor particular de la otra, es Gaussiana. Los parámetros
para estas distribuciones Gaussianas condicionales pueden calcularse a partir de los 5
parámetros de la normal bivariada. Para la distribución de x dado un valor particular de
y, la función de densidad condicional
tiene los siguientes parámetros:
Ejemplo 4.7, pag. 94
Distribución Gamma
Las distribuciones estadísticas de muchas variables atmosféricas son
claramente asimétricas y sesgadas a la derecha (existe un límite físico
a la izquierda), por ejemplo la precipitación o la rapidez del viento, las
cuales no pueden tomar valores negativos.
Una distribución que se utiliza comúnmente para representar datos de
precipitación es la distribución Gamma, que está definida por la PDF:
α se conoce como el parámetro
de la forma (adimensional)
β se conoce como el parámetro
de escala (tiene las mismas
dimensiones físicas que x).
• La función
está definida como:
la cual se evalúa numéricamente o usando tablas.
• Satisface la relación de recurrencia factorial:
• La media de la distribución gamma está dada por µ = αβ y la varianza
es σ2 = αβ2.
• Ejercicio: Usar el Método de Momentos para obtener estimadores de
los parámetros de la distribución Gamma.
• Sin embargo, en este caso, los estimadores calculados por el Método de
Momentos son buenos solamente para valores grandes de α.
• Una mejor aproximación se obtiene con el Método de Máxima Verosimilitud
con el cual se obtienen los siguientes estimadores para los parámetros de la
distribución Gamma:
• La PDF gamma no se puede integrar analíticamente. Las
probabilidades se pueden calcular mediante aproximaciones a la CDF
o a partir de valores tabulados que están disponibles para la
distribución Gamma estándar, con β = 1. Se debe reescalar la variable
X de interés (caracterizada por una distribución gamma con
parámetro β arbitrario) usando la transformación:
El parámetro alfa será el mismo para x y
Evaluación cualitativa de la bondad de ajuste
• El método más simple e intuitivo de comparar una distribución paramétrica
con los datos subyacentes es la superposición de la distribución ajustada al
histograma.
• El área bajo la curva de la PDF es igual a 1, por lo tanto debemos reescalar la
PDF.
• El área ocupada colectivamente por todas las barras en el histograma es igual
a A = No. total de observaciones x ancho de clase (para el caso de frecuencias
absolutas). Por lo tanto tenemos que multiplicar la PDF por A para que sea
equivalente al histograma.
• Si usamos las frecuencias relativas y el ancho de clase es distinto de 1,
tenemos que multiplicar la PDF por el ancho de clase. También es posible
reescalar las alturas de las barras para que el área total contenida en el
histograma sea 1.
• Ejercicio (ejemplo 4.8 Wilks): Calcular los parámetros de la distribución
Gamma para los datos de precipitación de la Tabla A.2 utilizando las dos
fórmulas para los estimadores. Trazar el histograma para las frecuencias
relativas y ajustar las distribuciones Gamma obtenidas.