función Q
Anuncio

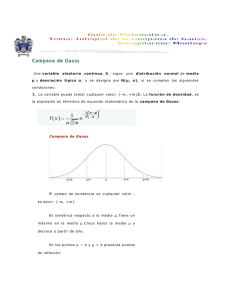
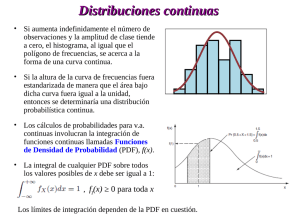
Sea X una variable aleatoria N(0,1), es decir, Gaussiana de media nula y varianza unitaria. Su función densidad de probabilidad es 1 − x2 / 2 , f X ( x) = e 2π y su función de distribución (Función de Distribución Gaussiana Normalizada, G(x)) es x x 1 −u 2 / 2 G ( x) = ∫ f X (u )du = ∫ e du . −∞ − ∞ 2π Se define la Función de Distribución Complementaria Gaussiana Normalizada, Q(x), como ∞ ∞ x x Q( x) = ∫ f X (u )du = ∫ 1 2π −u 2 / 2 e du = 1 − G ( x) fX(x) N(0,1) Q(x) x 0 Los valores la función Q(x) están tabulados, y se representan en la siguiente gráfica 0 10 -1 10 -2 10 -3 Q(x) 10 -4 10 -5 10 -6 10 -7 10 0 0.5 1 1.5 2 2.5 x 3 3.5 4 4.5 5