Laboratorio 1
Anuncio

UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA
“ANTONIO JOSÉ DE SUCRE”
VICE-RECTORADO PUERTO ORDAZ
LAB. DE TELECOMUNICACIONES
Sección de Comunicaciones
Laboratorio I
Análisis de Señales
En primer lugar, vamos a distinguir entre las magnitudes: amplitud A, frecuencia f y fase φ
en la función armónica. Utilizando MatLab.
x=Asin(2πf·t+φ).
1.
Trabajaremos con dos amplitudes distintas, A=10 y A=5 y la misma frecuencia
f=100 Hz, (el tiempo se mide en milisegundos, ms). Escriba el siguiente código en
Matlab.
subplot(2,1,1)
t=0:0.1:50;
x=10*sin(2*pi*0.1*t); %amplitud 10
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Distinta amplitud')
ylim([-11,11])
grid on
subplot(2,1,2)
x=5*sin(2*pi*0.1*t); %amplitud 5
plot(t,x,'r')
ylim([-10,10])
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on
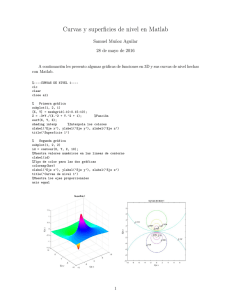
Debemos obtener graficas como las que observamos a continuación. Establezca sus
conclusiones con respecto a la actividad realizada.
2.
Ahora mantendremos la misma amplitud A=10, con dos frecuencias distintas f=100
y f=200 Hz
subplot(2,1,1)
t=0:0.1:50;
x=10*sin(2*pi*0.1*t); %frecuencia, 100 Hz
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Distinta frecuencia')
ylim([-11,11])
grid on
subplot(2,1,2)
x=10*sin(2*pi*0.2*t);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on
%frecuencia, 200 Hz
Debemos obtener graficas como las que observamos a continuación. Establezca sus
conclusiones con respecto a la actividad realizada.
3.
Siguiendo con la mismo orden de ideas, ahora cambiaremos la fase, utilizaremos
fases distintas: 0, π/2, π,3π/2, misma frecuencia f=100 Hz y misma amplitud A=10
subplot(4,1,1)
t=0:0.1:50;
x=10*sin(2*pi*0.1*t);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Distinta fase inicial')
ylim([-11,11])
grid on
subplot(4,1,2)
x=10*sin(2*pi*0.1*t+pi/2);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on
subplot(4,1,3)
x=10*sin(2*pi*0.1*t+pi);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on
subplot(4,1,4)
x=10*sin(2*pi*0.1*t+3*pi/2);
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
ylim([-11,11])
grid on
Debemos obtener graficas como las que observamos a continuación. Establezca sus
conclusiones con respecto a la actividad realizada.
4.
Una función periódica es el resultado de la superposición de tres funciones
armónicas con distintas frecuencias, amplitudes y fases. Se trabajara con la
siguiente ecuación:
x=200sin(2πf·100+π/2)+100sin(2πf·200+π)+100sin(2πf·400+3π/2)
La desarrollaremos en Matlab con el siguiente código
f=[100,200,400]; %frecuencias
A=[200,100,100]; %amplitudes
phi=[90,180,270]; %fases
subplot(2,2,1)
stem(f,A)
axis([0,500,0,210])
xlabel('Frecuencia')
ylabel('Amplitud')
subplot(2,2,2)
stem(f,phi)
axis([0,500,0,360])
xlabel('Frecuencia')
set(gca,'YTick',0:90:360)
set(gca,'YTickLabel',{'0',90','180','270','360'})
ylabel('Fase')
subplot(2,2,3:4) %resultante
t=(0:0.1:30)/1000; %milisegundos
x=zeros(1,length(t));
for i=1:length(f)
x=x+A(i)*sin(2*pi*f(i)*t+phi(i)*pi/180);
end
plot(t,x,'r')
xlabel('t(ms)')
ylabel('x')
title('Resultante')
ylim([-410,410])
set(gca,'XTick',(0:5:30)/1000)
set(gca,'XTickLabel',{'0','5','10','15','20','25','30'})
grid on
Debemos obtener graficas como las que observamos a continuación. Establezca sus
conclusiones con respecto a la actividad realizada.