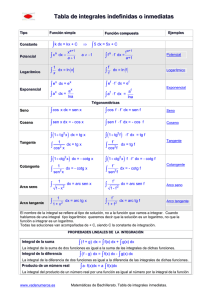
Tabla de integrales inmediatas
Anuncio

UNIVERSIDAD DE MURCIA DEPARTAMENTO DE MATEMÁTICAS MATEMÁTICAS I. GRADO EN QUÍMICA Integrales inmediatas un+1 n+1 1. R un du = 2. R du u 3. R eu du = eu + C 4. R au du = 5. R sen u du = − cos u + C 6. R cos u du = sen u + C 7. R csc u du = − ln | csc(u) + cot(u)| + C 8. R sec u du = − ln | sec(u) + tan(u)| + C 9. R du sen2 u = − cot u + C 10. R du cos2 u = tan u + C 11. R senh u du = cosh u + C 12. R cosh u du = senh u + C 13. R du senh2 u = coth u + C 1 senh2 u = coth2 u − 1 14. R du cosh2 u = tanh u + C 1 cosh2 u = 1 − tanh2 u 15. R √ du 1−u2 = arc sen u + C 16. R √−du 1−u2 = arc cos u + C 17. R du 1+u2 con n 6= −1 +C = ln |u| + C au ln a +C con a > 0, a 6= 1 1 sen2 u 1 cos2 u = arctan u + C 1 = 1 + cot2 u = 1 + tan2 u Formulario de integración 18. R √ du u2 +1 19. R √ du u2 −1 20. R du 1−u2 √ = argsenh u + C = ln |u + 1 + u2 | + C √ = argcosh u + C = ln |u + u2 − 1| + C = argtanh u + C Observaciones. 1. Del hecho de que 1 = sen2 u + cos2 u se desprende que 1 = 1 + cot2 u sen2 u 1 = 1 + tan2 u cos2 u 2. Del hecho de que 1 = cosh2 u − senh2 u se desprende que 1 = coth2 u − 1 senh2 u 1 = 1 − tanh2 u cosh2 u 1. Cambios de variable notables R dx 1. Si I = ax2 +bx+c , y r = p ± ıq son las raı́ces del denominador entonces hacemos el cambio t = x−p q obteniendo Z 1 dt I= . 2 aq t +1 R√ 2. Si I = a2 − x2 dx hacemos u = arc sen( xa ) y obtenemos x p a2 I= arc sen + x a2 − x2 + C. 2 a 2. Fórmulas de reducción 1. Si In = R cosn (u) du entonces In = 2. Si In = R senn (u) du entonces In = 3. Si I = 1 n−1 sen(u) cosn−1 (u) + In−2 . n n du (1±u2 )n 1 n−1 cos(u) senn−1 (u) + In−2 . n n entonces In = u 2n − 3 + In−1 . 2 n−1 2(n − 1)(1 ± u ) 2n − 2 2 3. Integral definida Teorema 1. Si Rf (x) es una función integrable en un intervalo [a, b] y hax cemos F (x) = a f (t)dt entonces F (x) es derivable en [a, b] y se tiene F 0 (x) = f (x). Teorema 2. Si f (x) es una función integrable en un intervalo [a, b] y R Rb F (x) = f (t)dt es cualquier primitiva entonces a f (x)dx = F (b) − F (a). 4. Aplicaciones Sólo aparecen aquellas aplicaciones que tienen una fórmula directa. Los métodos se tienen en los apuntes. 4.1. Sea Curvas en forma paramétrica ( x = f1 (t) C: y = f2 (t) t ∈ [t0 .t1 ]. entonces el área debajo de la superficie determinada por la curva y el intervalo es Z t1 A= f2 (t)f10 (t)dt. t0 4.2. Curvas en forma polar Si f (α) es una función sobre un ángulo α integrable entonces el área determinada por la función y las rectas de ángulos θ1 y θ2 es Z θ1 A= f2 (α)2 dα. θ0 4.3. Longitud de una curva Si f (x) es una función con una curva continua en el intervalo [a, b] entonces la longitud de la curva en dicho intervalo es: Z bq 1 + (f 0 (x))2 dx. L= a 4.4. Volúmenes de sólidos de revolución Si f (x) es continua, con f (x) ≥ 0 en [a, b] el volumen del sólido de revolución generado por la curva en el intervalo es Z b V =π f (x)2 dx. a 3