Integrales Indefinidas: Tabla
Anuncio
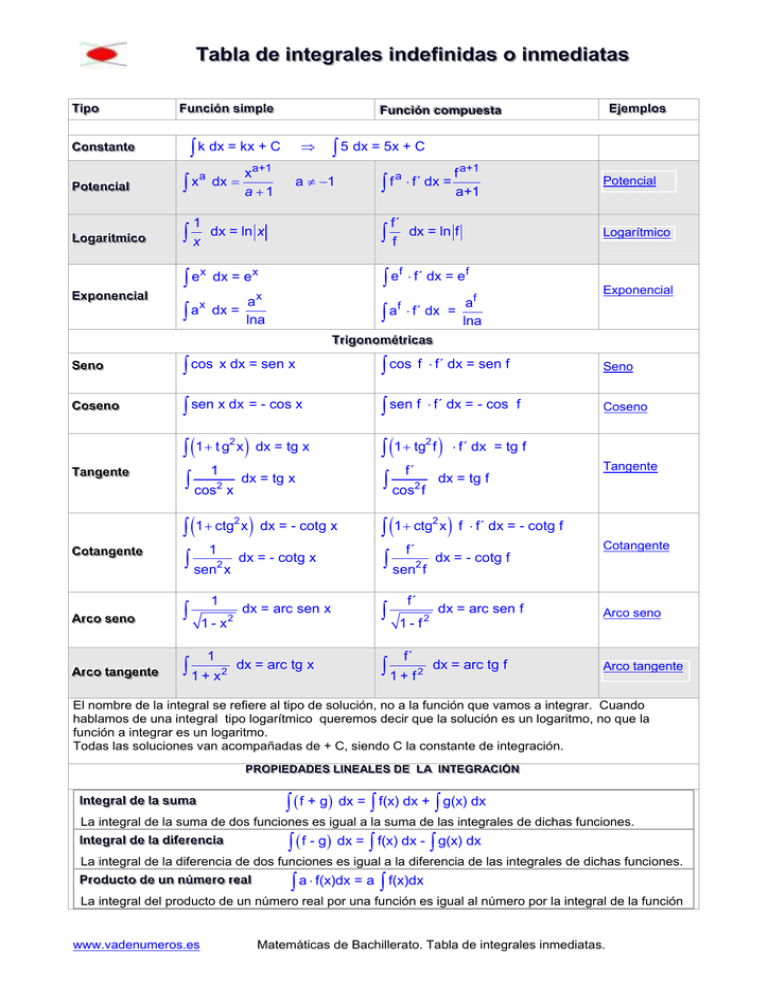
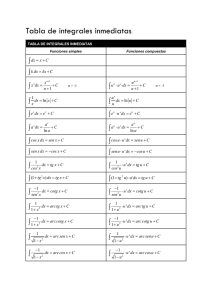
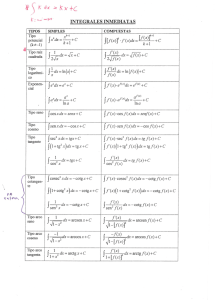
TTaabbllaa ddee iinntteeggrraalleess iinnddeeffiinniiddaass oo iinnm meeddiiaattaass T T p o Tiiip po o F F u n ó n m p Fu un nccciiió ón n sssiiim mp pllleee ∫ k dx = kx + C C C o n n Co on nssstttaaan nttteee P P o n Po ottteeen nccciiiaaalll a ∫ x dx = L L o g m o Lo og gaaarrrííítttm miiiccco o ∫x 1 E E p o n n Exxxp po on neeen nccciiiaaalll ∫e x E E m p o Ejjjeeem mp plllo osss F F u n ó n o m p u Fu un nccciiió ón n ccco om mp pu ueeessstttaaa ∫ 5 dx = 5x + C ⇒ xa+1 a +1 a ∫ f ⋅ f´ dx = a ≠ −1 f´ dx = ln x ∫f dx = e x ∫e ax a dx = ∫ lna f f a+1 a+1 dx = ln f Logarítmico ⋅ f´ dx = ef af a ⋅ f´ dx = ∫ lna x Potencial Exponencial f T T g o n o m Trrriiig go on no om mééétttrrriiicccaaasss S S n o Seeen no o ∫ cos x dx = sen x ∫ cos f ⋅ f´ dx = sen f Seno C C o n o Co ossseeen no o ∫ sen x dx = - cos x ∫ sen f ⋅ f´ dx = - cos f Coseno 2 ∫ (1 + t g x ) dx = tg x 2 ∫ (1 + tg f ) T T n g n Taaan ng geeen nttteee 1 ∫ cos2 x ∫ cos2 f 2 ∫ (1 + ctg x ) dx = - cotg x C C o n g n Co otttaaan ng geeen nttteee 1 ∫ sen2 x 1 A A o n o Arrrccco o ssseeen no o ∫ A A o n g n Arrrccco o tttaaan ng geeen nttteee ∫ 1 + x2 1- x 1 2 Tangente f´ dx = tg x ⋅ f´ dx = tg f dx = tg f 2 ∫ (1 + ctg x ) f f´ dx = - cotg x ∫ sen2 f dx = arc sen x ∫ Cotangente dx = - cotg f f´ dx = arc sen f 1 - f2 f´ ∫ 1 + f2 dx = arc tg x ⋅ f´ dx = - cotg f dx = arc tg f Arco seno Arco tangente El nombre de la integral se refiere al tipo de solución, no a la función que vamos a integrar. Cuando hablamos de una integral tipo logarítmico queremos decir que la solución es un logaritmo, no que la función a integrar es un logaritmo. Todas las soluciones van acompañadas de + C, siendo C la constante de integración. P E N A E D S E A E N S E D A D N E Ó P C O A R R P G GR EG DE NTTTE A IIIN E LLLA SD ES ALLLE EA NE S LLLIIIN ES DE AD DA N ED ÓN PIIIE CIIIÓ OP AC RO RA PR IIIn n g d u m nttteeeg grrraaalll d deee lllaaa sssu um maaa ∫ ( f + g) dx = ∫ f(x) dx + ∫ g(x) dx La integral de la suma de dos funciones es igual a la suma de las integrales de dichas funciones. IIIn n g d d n nttteeeg grrraaalll d deee lllaaa d diiifffeeerrreeen nccciiiaaa ( f - g) dx = f(x) dx - g(x) dx ∫ ∫ ∫ La integral de la diferencia de dos funciones es igual a la diferencia de las integrales de dichas funciones. P P o d u o d u n n ú m o Prrro od du ucccttto od deee u un nn nú úm meeerrro o rrreeeaaalll a ⋅ f(x)dx = a f(x)dx ∫ ∫ La integral del producto de un número real por una función es igual al número por la integral de la función www.vadenumeros.es Matemáticas de Bachillerato. Tabla de integrales inmediatas.