Trabajo Práctico Nº 6

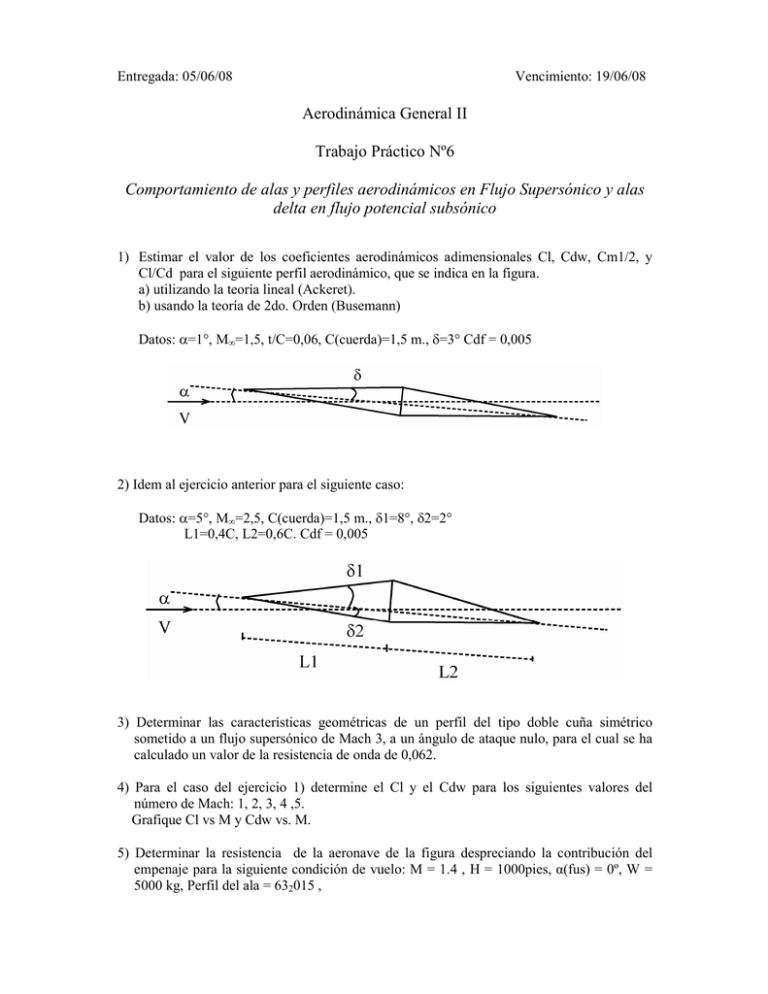
Entregada: 05/06/08
Vencimiento: 19/06/08
Aerodinámica General II
Trabajo Práctico Nº6
Comportamiento de alas y perfiles aerodinámicos en Flujo Supersónico y alas
delta en flujo potencial subsónico
1) Estimar el valor de los coeficientes aerodinámicos adimensionales Cl, Cdw, Cm1/2, y
Cl/Cd para el siguiente perfil aerodinámico, que se indica en la figura.
a) utilizando la teoría lineal (Ackeret).
b) usando la teoría de 2do. Orden (Busemann)
Datos: α=1°, M∞=1,5, t/C=0,06, C(cuerda)=1,5 m., δ=3° Cdf = 0,005
2) Idem al ejercicio anterior para el siguiente caso:
Datos: α=5°, M∞=2,5, C(cuerda)=1,5 m., δ1=8°, δ2=2°
L1=0,4C, L2=0,6C. Cdf = 0,005
3) Determinar las características geométricas de un perfil del tipo doble cuña simétrico
sometido a un flujo supersónico de Mach 3, a un ángulo de ataque nulo, para el cual se ha
calculado un valor de la resistencia de onda de 0,062.
4) Para el caso del ejercicio 1) determine el Cl y el Cdw para los siguientes valores del
número de Mach: 1, 2, 3, 4 ,5.
Grafique Cl vs M y Cdw vs. M.
5) Determinar la resistencia de la aeronave de la figura despreciando la contribución del
empenaje para la siguiente condición de vuelo: M = 1.4 , H = 1000pies, α(fus) = 0º, W =
5000 kg, Perfil del ala = 632015 ,
Datos geométricos:
L1 = 4.5 m
L2 = 5 m
L3 = 4.5 m
L4 = 11 m
b=9m
b2 = 0.2 m
b3 = 1 m
6) Dada la configuración en ala delta de una aeronave en mach 0.7 determinar mediante la
teoría potencial el coeficiente de sustentación y resistencia para dicha condición:
Datos:
C = 10 m
B=5m
a=2m
Cdo = 0.02
α = 2º
Cuestionario:
1) Explique las hipótesis de la teoría de pequeñas perturbaciones en flujo bidimensional
supersónico.
2) Que características generales deben cumplir los perfiles para ser aplicable dicha teoría.
3) Describa conceptualmente las leyes de áreas de primer orden y la de segundo orden.
4) ¿Cómo esta compuesta le resistencia total de una aeronave en vuelo supersónico?
Describa cada término.
5) ¿Cuáles son las diferencias entre la teoría de Ackeret y Busemann?
6) Explique conceptualmente las contribuciones a la sustentación en las alas deltas en
general.
Expresión para el cálculo de momentos respecto del punto X0
Cm X = ∑
0
i
 x −x
li c p i
cos ∆θ i  0 i
l cos δ i
 l

l c pi
 li

+∑ i
∆
θ
tang
δ
sen


i
i

δ
cos
2
l
l


i
 i
Coeficientes de sustentación y resistencia para un ala delta en flujo potencial
C L = K p senα cos 2 α + K v sen 2α cos α
C D − C D0 = C L tgα
C D = C D0 + K p sen 2α cos α + K v sen 3α