Práctica 1 CALORIMETRIA DIFERENCIAL DE BARRIDO
Anuncio
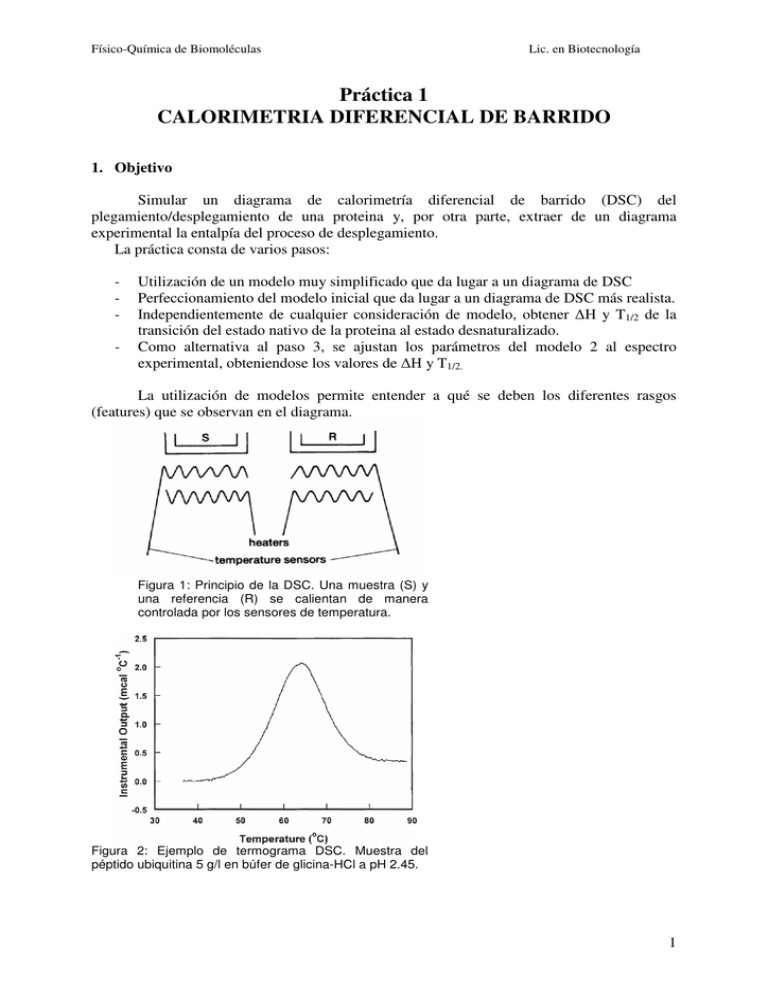
Físico-Química de Biomoléculas Lic. en Biotecnología Práctica 1 CALORIMETRIA DIFERENCIAL DE BARRIDO 1. Objetivo Simular un diagrama de calorimetría diferencial de barrido (DSC) del plegamiento/desplegamiento de una proteina y, por otra parte, extraer de un diagrama experimental la entalpía del proceso de desplegamiento. La práctica consta de varios pasos: - Utilización de un modelo muy simplificado que da lugar a un diagrama de DSC Perfeccionamiento del modelo inicial que da lugar a un diagrama de DSC más realista. Independientemente de cualquier consideración de modelo, obtener H y T1/2 de la transición del estado nativo de la proteina al estado desnaturalizado. Como alternativa al paso 3, se ajustan los parámetros del modelo 2 al espectro experimental, obteniendose los valores de H y T1/2. La utilización de modelos permite entender a qué se deben los diferentes rasgos (features) que se observan en el diagrama. Figura 1: Principio de la DSC. Una muestra (S) y una referencia (R) se calientan de manera controlada por los sensores de temperatura. Figura 2: Ejemplo de termograma DSC. Muestra del péptido ubiquitina 5 g/l en búfer de glicina-HCl a pH 2.45. 1 Físico-Química de Biomoléculas Lic. en Biotecnología 2. Fundamento La calorimetría diferencial de barrido (DSC) consiste en calentar una muestra (S en la Figura 1) así como un compuesto de referencia (R) de tal manera que la temperatura es en todo momento igual en R y en S. Esto se consigue midiendo las temperaturas con sensores y ajustando las potencias de calentamiento. Se aplican velocidades de calentamiento (en grados/s) uniformes a la muestra y a la referencia para realizar el barrido de temperaturas. La representación de la potencia de calentamiento frente a la temperatura es lo que se denomina diagrama DSC o, dado que se realiza frente a la temperatura, termograma. Un ejemplo de termograma se encuentra en la Figura 2. La DSC detecta transiciones que implican intercambio de energía, sea almacenamiento de calor (procesos endotérmicos) o liberación de calor (procesos exotérmicos). Ejemplos de estos procesos son las transiciones de fase (sólidosólido o sólido-líquido por ejemplo), procesos de cristalización, oxidaciones irreversibles, deshidrataciones, etc… Esta técnica también resulta muy adecuada para comprobar la pureza de un material, examinando la forma y la anchura del pico obtenido. Para muestras biológicas, esta técnica está considerada hoy en día como la más adecuada para estudiar la energética de las transiciones plegamiento-desplegamiento de las proteinas. Permite la caracterización termodinámica de los cambios conformacionales inducidos por cambios de temperatura en proteinas, ácidos nucléicos y biomembranas. Un aspecto fundamental para la modelización que efectuaremos en esta práctica es que supondremos que el sistema se encuentra en todo momento en equilibrio termodinámico, lo que correspondería a una velocidad de barrido infinitamente lenta. Consideremos una proteína que puede estar en uno de dos estados: Nativo (N) y Desnaturalizado (U). Estos estados están en equilibrio. Sea la fracción molar de proteina desnaturalizada. N ↔ U C (1- )C La constante de equilibrio de esta reacción es: [U ] K = (1) [N ] αC α K = = (2) (1 − α)C 1 −α La Ecuación (2) puede escribirse para expresar K α = (3) 1 + K en función de K: Dado que medimos el calor que se le proporciona a la muestra comparandolo con una muestra de referencia que no contiene la proteína, el primer principio de la termodinámica dicta que: Q = ∆H R = (1 − α)CV C pN dT + αCV∆H + αCV C pU dT − CV C p0dT (4) En esta ecuación, Q es la cantidad de calor que se le proporciona a la muestra, HR es la variación de entalpía del sistema, C la concentración de la proteína, V el volumen de la muestra, H la entalpía molar para pasar de la proteína nativa a la desnaturalizada a una temperatura de referencia Tm (luego veremos qué valor de Tm es oportuno elegir), CpN, CpU y Cp0 serían la capacidad calorífica de la proteína nativa, desnaturalizada, y de una cantidad de agua que ocupe el mismo volumen que la proteina. Las integrales se realizan entre Tm y T. 2 Físico-Química de Biomoléculas Lic. en Biotecnología Puesto que el número de moles de proteínas es n = CV , (5) la Ec. 4 puede escribirse como: Q = n α ∆H + (C pU − C pN )dT + (C pN − C p 0 )dT , ( (( ) ) ) (6) donde ∆H + (C pU − C pN )dT es una entalpía molar corregida por la temperatura, que se conoce como relación de Kirchoff: ∆H(T) = ∆H(Tm ) + T ∆C p(T')dT' (7) Tm donde Cp(T´)= CpU(T´)- CpN(T´). Se supone que CpN y Cp0 no varían mucho con la temperatura por lo que se pueden “sacar” de la integral. Q = (α∆H(T) + (C pN − C p0)∆T )n (8) T es la diferencia (T-Tm). Ahora derivamos la ec. (4) con respecto al tiempo: dQ d(α∆H) dT (9) = + (C pN − C p0) n dt dt dt Sabiendo que d(α∆H) d(α∆H) dT = , dt dT dt Podemos sacar factor común de dT/dt en la ec. (9). Para entender la ec. 9, recordemos que dT/dt= es la velocidad constante a la que se efectúa el calentamiento en K/s y dQ/dt=P(T) es la potencia que suministra el calorímetro. En consecuencia, la ec. (9) se transforma en: P(T) d(α∆H) = + C pN − C p0 (10) nσ dT El diagrama consta de un “cero” al que se llamara base (y de unas desviaciones del cero (picos). Pbase(T) (11) = C pN − C p0 nσ Pxs(T) d(α∆H) = (12) nσ dT Los términos a la derecha de la igualdad en la ec. 12 son formalmente capacidades caloríficas. El término de la izquierda corresponde entonces a una capacidad calorífica aparente de exceso Cp,xs d(α∆H) C p,xs(T) = (13) dT La Ec. 12 expresa que la parte que resulta de interés en el diagrama, las desviaciones de la base, es proporcional a la capacidad calorífica de exceso de la proteína. Nuestro cometido es, por tanto, obtener una representación de Cp,xs(T). Para conocer K, que se necesita en la ec. (3), se utiliza la relación de van´t Hoff: 3 Físico-Química de Biomoléculas d(ln K ) ∆H = dT RT 2 Lic. en Biotecnología (14) A continuación vamos a suponer que CpU=CpN de modo que H(T) es independiente de la temperatura= H. Ec. (14) puede integrarse: 2 2 ∆H d(ln K ) = dT RT 2 1 1 ln K(T2) ∆H 1 1 = − K(T1) R T1 T2 ∆H 1 1 − R T1 T2 K(T2) = K(T1)e (15) Por definición, la temperatura T1/2 es aquella para la que =0.5 (es decir K(T1/2)=1, ec. (2)). Usaremos esta temperatura como referencia en la ec. (14) y T2=T. Nota, T1/2 es normalmente identico a Tm, el máximo de la capacidad calorífica de exceso en el diagrama de DSC. Ec (14) se simplifica: K(T) = e ∆H 1 1 − R Tm T Volvamos a la ec. (12). En el caso de este primer modelo, se reduce a: d(α∆H) C p,xs(T) = dT d(α) = ∆H dT Las derivadas se obtienen de forma numérica: dα α(T + δT) − α(T − δT) = dT (T + δT) − (T − δT) α(T + δT) − α(T − δT) = 2δT Sustitución de (17) en (16): C p,xs(T) = α(T + δT) − α(T − δT) ∆H 2δT (16) (17) (18) (19) 3. Procedimiento práctico Primero se crea una carpeta de trabajo en el Escritorio en la que se guardarán todos los ficheros. 1) En una hoja de cálculo de Excel, se dedican unas celdas a los datos de entrada. Introducir los datos en las unidades indicadas: H /kJmol-1, T1/2 /K, T /K, y a la constante R=0.008314 kJ/mol. Para todos los casos se usará T=10-6 K 4 Físico-Química de Biomoléculas Lic. en Biotecnología En la hoja de cálculo, por debajo de las celdas de datos, se usarán las columnas A-H para los datos siguientes: A B Temperaturas T+ T T /K 273 274 … 373 C T- T D K(T+ T) E K(T- T) F (T+ T) G H (T- T) Cp,xs La columna de las temperaturas es una columna de datos que hay que generar: se quieren calcular las temperaturas de 273 a 373 K cada Kelvin. Las columnas D y E se obtienen con la ec. (16); las columnas F y G a partir de la ec. (3); la columna H finalmente a partir de la ec. (19). a) Caso 1: T1/2=300 K, H=200 kJ/mol Obtener los valores de Cp,xs, copiarlos en una columna distinta. Sugerencia: se puede usar copiar y “ pegado especial” convirtiendo las fórmulas a Valores. De esta manera, los datos no se actualizarán si se modifica el contenido de la celda que contiene H. b) Caso 2: T1/2=300 K, H=100 kJ/mol Representar los datos en una gráfica XY de dispersión en una Hoja aparte. Elegir una escala adecuada (250-400 K). Comparar los diagramas entre sí. Compararlos también con el diagrama DSC de la ubiquitina (Figura 2). 2) Obtención de H y Tm de un registro de DSC experimental Tm es la temperatura a la que la capacidad calorífica de exceso es máxima. H se obtiene por integración por trapecios del pico asumiendo que la línea base es una recta. Abrir una nueva hoja que llamaremos Hoja 3. Conectarse a la página web de la asignatura (http://www.upo.es/depa/webdex/quimfis/quimbiotec_FQbiomol.html). Junto a la práctica de la DSC, se encuentra un fichero de datos DSCexp.dat. Descargar este fichero y guardarlo en la carpeta de trabajo. Abrir este fichero con Excel. Copiar los datos a columnas seleccionadas de la Hoja 3. Representar los datos en una gráfica XY de dispersión en una Hoja nueva que llamaremos Gráfico 3. Seleccionar a ojo dos puntos de la curva por los que pasará también la línea base (un punto de principio (X0,Y0) y uno de fin del pico (X1,Y1)). En una columna obtener para cada temperatura la ordenada de la línea base. Integrar el pico entre X0 e X1 según el método de los trapecios para obtener H. 5 Físico-Química de Biomoléculas Lic. en Biotecnología 3) Obtención de H y Tm de un registro de DSC experimental ajustandolo al Modelo 1 En este caso vamos a determinar los parámetros de tal manera que el Modelo 1 se ajuste lo mejor posible a los datos experimentales. Estos datos comportan dos columnas, las temperaturas en K y las capacidades caloríficas de exceso en kJ/mol. Copiar la Hoja 1 a una nueva Hoja de cálculo que llamaremos Hoja 4. Ahora, H y Tm no se considerarán datos sino estimaciones iniciales y dejaremos que Excel los modifique durante el ajuste. Del fichero de datos copiado de la página web y que se trata de ajustar, copiar la columna de temperaturas a la columna A (de manera que el Modelo proporcione los datos de Cp,xs a los intervalos en los que se dispone también de datos experimentales). En otra columna, copiamos los Cp,xs experimentales. Construiriamos entonces la función de la suma de los cuadrados de la diferencia entre Cp,xs experimental y calculado: R = (C p,xs exp − C p,xscalc)2 No obstante, el Modelo 1 presenta ciertas deficiencias, así que optamos por dotarlo de una linea base ajustable de forma que la nueva función calculada queda como: C p , xscalcnuevo = C p , xscalc + c 1 + arctan( T − Tm ) d Con la herramienta “ solver” de Excel (comprobar que su versión de Excel haya sido instalada con este módulo), se minimiza esta función utilizando las casillas H, Tm, c y d. Es importante que las estimaciones iniciales se encuentren razonablemente cerca de la solución. De no ser así, el programa puede converger hacia una solución que no es la correcta. Este es un problema muy general en la minimización de funciones de varias variables. Es muy fácil encontrar un “ mínimo local” pero de forma general, no existe ningún método para encontrar con fiabilidad el mínimo absoluto de la función. Opcionalmente se puede representar la función ajustada frente al diagrama experimental. Probar por ejemplo el conjunto de valores iniciales: H=150 kJ/mol , Tm= 290 K, c=1 y d=1, cuya minimización debería dar un R "pequeño" y una muy buena adecuación a la curva. Cambiar ahora el valor de la temperatura inicial a 280 K y observar la nueva solución. 6 Físico-Química de Biomoléculas Lic. en Biotecnología Figura 3: Problemática de encontrar el mínimo global de una función de varias variables Nota: Los valores “ reales” de la curva DSC son H=200 kJ/mol y Tm=300 K. 7. Bibliografía Michael E. Brown, Introduction to Thermal Analysis, 2nd ed., Techniques and Applications, Secaucus, NJ USA: Kluwer Acad., 2001; libro electrónico Babur Chowdhry y Stephen Leharne, Simulation and Analysis of Differential Scanning Calorimetry Output: Protein Unfolding Studies 1, J. Chem. Edu., 74, 236 (1997) 7