PROGRAMACIÓN DINÁMICA [A] DEFINICIÓN DE

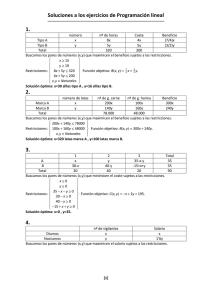
PROGRAMACIÓN DINÁMICA
[A] DEFINICIÓN DE PROGRAMACIÓN DINÁMICA.Técnica de programación matemática que proporciona un
procedimiento sistemático para determinar la combinación óptima de
una serie de decisiones interrelacionadas.
[B] CONCEPTUALIZACIÓN DE PROGRAMACIÓN DINÁMICA.1. En contraste con la programación lineal, no se cuenta con una
formulación matemática estándar para “el” problema de
Programación dinámica.
2. Se trata de un enfoque de tipo general para la solución de
problemas y las ecuaciones específicas que se usan se deben
desarrollar para que representen cada situación individual.
3. Se necesita un cierto grado de creatividad y un buen conocimiento
de la estructura general de de los problemas de Programación
Dinámica para reconocer cuándo y cómo se puede resolver un
problema por medio de estos procedimientos.
[C] TIPOS DE PROGRAMACIÓN DINÁMICA.1. Programación dinámica determinística.
El estado en la siguiente etapa está completamente determinado por
el estado y la política de decisión de la etapa actual.
2. Programación dinámica probabilística.
El estado en la siguiente etapa no está completamente determinado
por el estado y la política de decisión de la etapa actual, existiendo
en su lugar una distribución de probabilidad para determinar cuál
será el siguiente estado.
[D] CARACTERÍSTICAS DE PROGRAMACIÓN DINÁMICA.1. Etapas:
El problema se puede dividir en etapas que requieren una política de
decisión en cada una de ellas.
2. Estados asociados:
Cada etapa tiene cierto número de estados asociados con su inicio.
3. Política de decisión:
El efecto de la política de decisión en cada etapa es transformar el
estado actual en un estado asociado con el inicio de la siguiente
etapa.
4. Diseño de solución:
El procedimiento de solución está diseñado para encontrar una
política óptima para el problema completo, es decir, una receta para
la política de decisión óptima en cada etapa para cada uno de los
estados posibles.
5. Principio de optimalidad:
a. Dado el estado actual, una política óptima para las etapas
restantes es independiente de la política adoptada en etapas
anteriores.
b. La decisión inmediata óptima depende sólo del estado actual y
no de cómo se llegó ahí.
6. Inicio de solución:
El procedimiento de solución se inicia al encontrar una política
óptima para la última etapa.
7. Relación recursiva:
Se dispone de una relación recursiva que identifica la política óptima
para la etapa n, dada la política óptima para la etapa n + 1.
8. Retroceso:
Cuando se use esta relación recursiva, el procedimiento de solución
comienza al final y se mueve hacia atrás etapa por etapa –
encontrando cada vez la política óptima para esa etapa – hasta que se
encuentra la política óptima desde la etapa inicial.
PROBLEMA DE PROGRAMACIÓN DINÁMICA
Fundición Precisión
La fundición Precisión tiene 11 órdenes por moldes que deben ser
entregados en las próximas cuatro semanas.
Sus hornos e instalaciones de moldeo son normalmente usados para la
producción regular de moldes estándar, pero también pueden ser
programados para usarse si se presentan cuatro órdenes especiales por
semana.
Los costos de operación varían un poco dependiendo del número de
trabajos especiales que la empresa trata de producir en ese lapso.
Esto se debe a que la preparación del molde, calentamiento requerido de los
hornos, requerimientos de inventarios y tiempo extra tienden a variar.
Si no se hacen trabajos especiales, sin embargo, las instalaciones tienen un
costo asignado de tiempo ocioso.
Considerando los diferentes costos, así como el ingreso de unidades
especiales, se ha derivado la siguiente tabla de utilidades:
Tabla
Número de unidades N
(producidas en el período)
0
1
2
3
4
Utilidad ($00) de producir N
unidades en el período (semanas)
A
B
C
D
−4
−4
−4
−4
4
9
8
3
12
10
15
11
20
22
20
20
18
16
24
18
Úsese un enfoque de programación dinámica para programar la producción
de las 11 unidades sobre los cuatro períodos, en tal forma que se
maximicen las utilidades de la fundición.