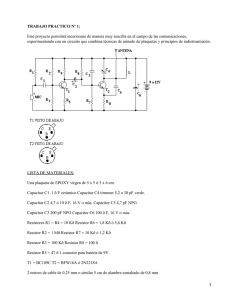
1.1. Divisor de voltaje y corriente.
Anuncio

1.1. Divisor de voltaje y corriente. Los dos resistores están en serie, ya que en ambos fluye la misma corriente i. Al aplicar la ley de Ohm a cada uno de los resistores se obtiene Si se aplica la LTK al lazo (desplazándonos en el sentido de las manecillas del reloj), se tiene Combinando las ecuaciones Para determinar la tensión a lo largo de cada resistor de la figura se sustituye la ecuación en la ecuación y se obtiene Obsérvese que la tensión en la fuente v se divide entre los resistores en proporción directa a sus resistencias; a mayor resistencia, mayor caída de tensión. Esto se llama principio de división de tensión En general, si un divisor de tensión tiene N resistores R1, R2, . . . , RN) en serie con la tensión en la fuente v, el nésimo resistor (Rn) tendrá una caída de tensión de Resistores en paralelo y división de corriente Considérese el circuito de la figura donde dos resistores están conectados en paralelo y por lo tanto tienen la misma tensión. Con base en la ley de Ohm, La aplicación de la LCK al nodo a produce la corriente total i como Al sustituir la ecuaciónes A menudo es más conveniente usar la conductancia en vez de la resistencia al tratar con resistores en paralelo. Partiendo de la ecuación la conductancia equivalente para N resistores en paralelo es ¿cómo se obtienen las corrientes i1 e i2? Se sabe que el resistor equivalente tiene la misma tensión Lo que indica que la corriente total i es compartida por los resistores en proporción inversa a sus resistencias. Esto se conoce como principio de división de corriente, y el circuito de la figura se conoce como divisor de corriente. Nótese que la corriente mayor fluye por la resistencia menor. Transformación de fuentes Recuérdese que un circuito equivalente es aquel cuyas características de v-i son idénticas a las del circuito original. En análisis de circuitos es útil poder sustituir una fuente de tensión en serie con un resistor por una fuente de corriente en paralelo con una resistencia o viceversa, como se muestra en la figura Transformación de fuentes independientes. Cualquier sustitución se conoce como transformación de fuente. Los dos circuitos de la figura anterior son equivalentes, en tanto tengan la misma relación tensión-corriente en las terminales a-b. Es fácil demostrar que en efecto son equivalentes. Si las fuentes se apagan, la resistencia equivalente en las terminales a-b en ambos circuitos es R. Asimismo, cuando las terminales a-b están en cortocircuito, la corriente correspondiente que fluye de a a b es isc=vs/R en el circuito de la izquierda e isc=is en el de la derecha. Así, vs/R=is para que ambos circuitos sean equivalentes. La transformación de fuente requiere que La transformación de fuentes también se aplica a fuentes dependientes, siempre y cuando se maneje con cuidado la variable dependiente. Como se muestra en la figura, una fuente de tensión dependiente en serie con un resistor puede transformarse en una fuente de corriente dependiente en paralelo con el resistor o viceversa, confirmando que se satisfaga la ecuación Transformación de fuentes dependientes. Una transformación de fuente no afecta a la parte restante del circuito. Se deben tener en cuenta los siguientes puntos al tratar con la transformación de fuentes. 1. Como se advierte en la figura la flecha de la fuente de corriente apunta hacia la terminal positiva de la fuente de tensión. 2. Como se deduce de la ecuación la transformación de fuente no es posible cuando R=0, el cual es el caso de una fuente de tensión ideal. Sin embargo, en una fuente de tensión real no ideal, De igual forma, una fuente de corriente ideal con no puede remplazarse por una fuente de tensión finita. Solución: Primero hay que transformar las fuentes de corriente y de tensión figura b) La combinación de los resistores de 4 y 2 en serie y la transformación de la fuente de tensión de 12 V dan por resultado la figura b). Ahora se combinan los resistores de 3 y 6 ohm en paralelo, para obtener 2 . Se combinan asimismo las fuentes de corriente de 2 y 4 A, para obtener una fuente de 2 A. Así, mediante la repetida aplicación de transformaciones de fuente, se obtiene el circuito de la figura c). Se aplica la división de corriente a la figura c), para obtener Alternativamente, puesto que los resistores de 8 y 2 de la figura c), están en paralelo, tienen la misma tensión vo entre sus extremos. Solución: El circuito de la figura incluye una fuente dependiente de corriente controlada por voltaje. Se transforma esta fuente de corriente dependiente, lo mismo que la fuente de tensión independiente de 6 V, como se indica en la figura a). La fuente de tensión de 18 V no se transforma, porque no está conectada en serie con ningún resistor. Los dos resistores de 2Ω en paralelo se combinan, para dar por resultado un resistor de 1Ω , el cual está en paralelo con la fuente de corriente de 3 A. La fuente de corriente se transforma en fuente de tensión, como se indica en la figura b). Obsérvese que las terminales de v están intactas. La aplicación de la LTK alrededor de la malla de la figura b) produce La aplicación de la LTK alrededor de la malla que contiene únicamente la fuente de tensión de 3v, el resistor de 1Ω y vx Alternativamente, se puede aplicar la LTK al lazo que contiene vx, el resistor de 4Ω , la fuente dependiente de voltaje controlada por tensión y la fuente de voltaje de 18 V en la figura b). De eso se obtiene Análisis de mallas.