CAPITALIZACIÓN SIMPLE 1. Calculénse el interés y el capital final

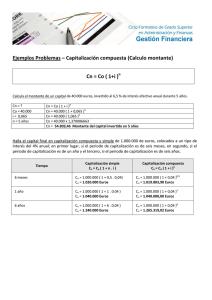
CAPITALIZACIÓN SIMPLE
1. Calculénse el interés y el capital final resultantes de invertir 10.000 euros durante
tres años a un tipo de interés anual del 5% en capitalización simple.
Interés:
Capital final:
I = C⋅i⋅n
C n = C ⋅ (1 + i ⋅ n )
2. Obténgase el capital final que resultará de invertir 12.000 euros durante 9 meses a un
tipos de interés anual del 4% en capitalización simple.
Solución: C n = 12.360 euros
1
3. Un capital inicial de 10.000 euros invertido durante 10 trimestres en capitalización
simple ha producido un capital final de 10.875 euros. Calcúlese el tipo de interés
anual que se le ha aplicado.
Para resolver este ejercicio se introduce en la celda C8 un valor arbitrario para el tipo de
interés anual (por ejemplo 5%) y en la celda C6 se calcula el capital final
correspondiente. A continuación, se utiliza la función Buscar objetivo (En
Herramientas), que nos permite resolver una ecuación con una incógnita, forzando a
que el valor del capital final (en C6) sea 10,875, con lo que se va a modificar la celda
que contiene nuestra incógnita (C8).
Tras pulsar Aceptar, aparece la siguiente pantalla, en la que se obtiene la solución
definitiva (tipo de interés anual del 3.5%).
2
4. El señor Pérez coloca en una cuenta financiera que abona intereses al 2.5% anual en
capitalización simple los siguientes capitales: 6.000 € en el momento de apertura de la
cuenta, 3.000 € un mes después y 6.000 dos meses después de este último. Determínese
el capital acumulado a los 6 meses de la apertura.
6000
3000
0
1
6000
2
3
4
5
6
3
CAPITALIZACIÓN COMPUESTA
5. Calcúlese el capital que se debería invertir en capitalización compuesta a un tipo de
interés efectivo anual del 4% para obtener en 4 meses un capital final de 9.900 €.
Este ejercicio se puede resolver, igual que el número 3 anterior, utilizando la función
Buscar objetivo.
6. Si colocando un capital de 9.000 €, en capitalización compuesta por semestres,
durante 5 años se obtiene un capital final de 11.700 €, obténgase el tipo de interés
efectivo semestral al que ha sido invertido, así como el tipo nominal anual y el tipo
efectivo anual equivalentes.
4
C13: =(1+C7)^(2)-1
C14: =2*C7
5
RENTAS
7. Calcúlese la cantidad a ingresar al final de cada año (anualidad) para constituir en 10
años un capital de 10.000 € si se valora con un tipo de interés efectivo anual del 4%.
Los valores del capital ahorrado se pueden obtener de dos formas. En primer lugar, con
la fórmula de capitalización aplicada año a año a lo que ya hay acumulado del año
anterior y sumándole lo aportado el año en curso (columna C). En segundo lugar,
utilizando la función financiera del valor final de una renta (VF), a la que se da como
argumentos el tipo de interés, el número de períodos y la cantidad entregada
periódicamente. Este último argumento aparece con signo negativo debido a que la hoja
de cálculo lo interpreta como un pago. Cambiando el signo de este argumento,
obtenemos el resultado esperado.
6
8. Determínese la cantidad que se debería depositar en un banco en el momento actual
para poder disfrutar durante 12 años de una renta anual constante al final de cada año de
5.000 € si se valora a un tipo de interés efectivo anual del 3%.
7
9. El señor Lucas realiza un ingreso de 3.000 € al final de cada semestre durante cinco
años en una entidad financiera que valora a un tipo de interés nominal anual del 3%
pagadero semestralmente. Calcúlese el capital ahorrado al final de los cinco años.
F4: =+F3/2, tipo de interés efectivo semestral (i(m)=j(m)/m)
C7: =+B7*(1+$F$4)^($F$2-A7), valor al final del semestre 10 del ingreso del sem. 1
C8: =+B8*(1+$F$4)^($F$2-A8), valor al final del semestre 10 del ingreso del sem. 2 y
así sucesivamente hasta C16
$F$4 el signo del dólar ($) se pone para que en todas las fórmulas se coja la casilla F4.
Con la casilla F2 ocurre lo mismo.
C18: =SUMA(C7:C16), suma del valor al final del semestre 10 de cada uno de los
ingresos semestrales.
C20: =B7*(((1+F4)^F2)-1)/F4, esta casilla contiene la fórmula del valor final de una
renta constante S n i . Para comprobar si los cálculos anteriores están bien efectuados.
8
CÁLCULO TANTO INTERNO DE RENDIMIENTO (TIR)
10. Para la compra de un coche de gama alta, cuyo precio al contado asciende a 35.000
€, nos ofrecen la posibilidad de pagar una entrada del 30% en el momento actual y 24
pagos mensuales de 1150 € al final de cada mes. Determínese el coste efectivo de la
financiación.
Para resolver este ejercicio se utiliza la función financiera TIR (tasa interna de
rentabilidad o tanto interno de rendimiento) de la hoja de cálculo.
La función TIR necesita dos argumentos. El primero es el rango de las celdas que
contienen la prestación y la contraprestación. En nuestro caso, van de la C3 a la C27, en
total 25 capitales, de los cuales el primero es la prestación y aparece con signo negativo
(-24.500 = -35.000 + 10.500) y el resto corresponden a los 24 pagos de la
contraprestación, que aparecen en positivo. Para que exista solución debe haber un
cambio de signo entre prestación y contraprestación. El segundo argumento es un tipo
de interés que sirve a la hoja de cálculo para arrancar en el cálculo.
En este caso, la solución que ofrece la TIR corresponde a un tipo de interés mensual, ya
que los capitales vencen mensualmente. Por ello, habrá que calcular el tipo de interés
efectivo anual equivalente al tipo mensual calculado por la función TIR.
Bibliografía.
Apraiz, A. (2003): Fundamentos de Matemática Financiera. Editorial Desclée de
Brouwer. Bilbao.
Cabello, J.M. et al. (1999): Matemáticas financieras aplicadas. Editorial AC. Madrid.
Hayat, S. y San Millán, A. (2001): Finanzas con Excel. McGraw-Hill. Madrid.
9