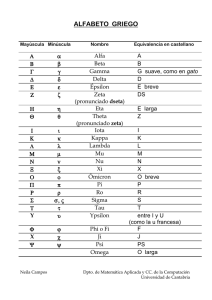
Año: 2.009 EPSILON DE LA COMPUTADORA: No importa cómo los
Anuncio

Año: 2.009 EPSILON DE LA COMPUTADORA: No importa cómo los números se almacenen, habrá un número, llamado el épsilon de la máquina, que será el menor número positivo que la computadora es capaz de almacenar. Cualquier número que ese épsilon será interpretado como igual a cero. En el ejemplo explicado más arriba el épsilon de la máquina es 10^(–99) ¿Por qué? La computadora no puede acercarse a 0 más que épsilon. • el número positivo "u" más pequeño tal que máquina es , llamado el epsilon de la (¿por qué?) Ejemplo. Usar el siguiente resultado de series, para aproximar el numero irracional hasta 4 cifras significativas. Solución. Primero calculamos el valor de como sigue: En seguida, usamos la serie, agregando un término cada vez, para obtener nuevas aproximaciones hasta que se logre que En el primer paso, tenemos simplemente un término: En el segundo paso, tenemos la suma de dos términos: Aquí, podemos calcular el primer error aproximado: . Año: 2.009 Seguimos agregando términos de la serie puesto que no se ha cumplido el objetivo: Tenemos que, Y calculamos el error aproximado correspondiente: El proceso se continua hasta lograr la meta. Resumimos los resultados en la siguiente tabla: # términos Aprox. al valor e Error aproximado 1 1 2 2 50% 3 2.5 20% 4 2.666666667 6.25% 5 2.708333333 1.54% 6 2.716666667 0.307% 7 2.718055556 0.051% 8 2.718253968 0.007% 9 2.718278770 0.0009% Así pues, el resultado que se obtiene es: Que en realidad tiene 8 cifras significativas. La cota impuesta por , nos asegura que tendremos al menos n cifras significativas; en este ejemplo, obtuvimos 4 cifras significativas más.