Document
Anuncio

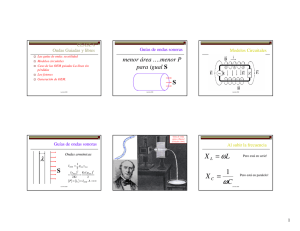
CLASE 8 Difracción Difracción significa cambio de dirección del rayo (vector de Poynting) de una onda debido a la interacción con un obstáculo Larrondo – Física 3 – 2010 Videos Caso Fraunhoffer laserRendija.mpg laserRendijaVar.mpg OEMrendija.mpg redes.mpg rendijasBlanca.mpg SingleSlit Larrondo – Física 3 – 2010 CLASE 11 Difracción Una explicación simple surge del principio de Huygens: “todo punto alcanzado por un frente de onda se comporta como un emisor secundario” Larrondo – Física 3 – 2010 CLASE 8 Difracción Al observador llegan los vectores de Poynting generados por esos emisores secundarios Larrondo – Física 3 – 2010 Rendija Rectangular Larga Difracción de Fraunhöfer Larrondo – Física 3 – 2010 Rendija Rectangular Larga Difracción de Fraunhöfer r0 0 x r0 + x sen θ θ r0 + d sen θ d Larrondo – Física 3 – 2010 Rendija Rectangular Larga Difracción de Fraunhöfer r0 0 x r0 + x sen θ θ r0 + d sen θ d Larrondo – Física 3 – 2010 kd sin θ kd sin θ Rendija Rectangular Larga Difracción de Fraunhöfer Para estos ángulos de observación I = 0 kd sin θ = 2 m π ⇒ d sin θ = λ ⇒ diagrama fasorial cerrado Larrondo – Física 3 – 2010 Sitio de Franco García: difracción. Larrondo – Física 3 – 2009 CLASE 11 Rendija Rectangular Larga Difracción de Fraunhöfer r0 0 x d r0 + x sen θ θ r0 + d sen θ φr = d ∫ 0 E i( k r0 + k x senθ − ω t ) i( k r0 − ω t + α ) sin α ⋅e dx = E ⋅ e d α kd sin θ α = 2 Larrondo – Física 3 – 2010 CLASE 8 Rendija Rectangular Larga Difracción de Fraunhöfer r0 0 x r0 + x sen θ θ r0 + d sen θ d I = I max sin 2 α 2 α Larrondo – Física 3 – 2009 kd sin θ α = 2 CLASE 11 Rendija Rectangular Larga Difracción de Fraunhöfer r0 0 x r0 + x sen θ θ r0 + d sen θ d I = I max sin 2 α 2 α Larrondo – Física 3 – 2010 kd sin θ α = 2 Diagramas polares vs. cartesianos OEMrendija.avi Larrondo – Física 3 – 2010 CLASE 11 Rendija Rectangular Larga Difracción de Fraunhöfer • Otro método: • Partir de la ecuación 3.2:07 de interferencia de N fuentes idénticas espaciadas ⎛ NkD ⎞ sin ⎜ sin θ ⎟ ⎝ 2 ⎠ E = E0 ⎛ kD ⎞ sin ⎜ sin θ ⎟ ⎝ 2 ⎠ Larrondo – Física 3 – 2010 CLASE 11 Rendija Rectangular Larga Difracción de Fraunhöfer • Calcular el límite N→∞ D→0 ND = d Larrondo – Física 3 – 2010 Determinación del ancho de una rendija a partir del diagrama de difracción Larrondo – Física 3 – 2010 Clase 12 Interferencia-Difracción de Fraunhoffer combinadas para rendijas rectangulares largas Difracción de Fresnel para abertura Circular Larrondo – Física 3 – 2009 Larrondo – Física 3 – 2009 Del patron de scattering podemos inferir cómo es el material Factor de Estructura ⎛ kd ⎞ sin ⎜ sin θ ⎟ ⎝ 2 ⎠ ⎛ kD ⎞ sin ⎜ N sin θ ⎟ 2 ⎝ ⎠ ⎞ 2 ⎛ kD sin ⎜ sin θ ⎟ ⎝ 2 ⎠ 2 I (θ ) = I max ⎛ kd ⎞ ⎜⎝ 2 sin θ ⎟⎠ 2 2 Factor de forma Larrondo – Física 3 – 2010 Larrondo – Física 3 – 2009 Larrondo – Física 3 – 2010 Deduzca la estructura de las rendijas redes.mpg De cada imagen deducir cómo está hecha la diapositiva Larrondo – Física 3 – 2010 • Todos estos diagramas de intensidad son estacionarios • Su forma se demuestra empleando fasores • Corresponden a la configuración de Fraunhoffer • VER EJEMPLOS FRANCO GARCÍA Larrondo – Física 3 – 2010 Larrondo – Física 3 – 2009 Fin clase 8 Larrondo – Física 3 – 2010