“Ordinary Least Square” (OLS) Método de Cuadrados
Anuncio

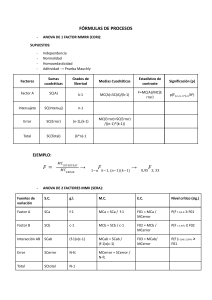
6 – septiembre – 2007 1 factor: Regresión “Ordinary Least Square” (OLS) Método de Cuadrados Mínimos y = β0 + β1x + ε factor: cualitativo vs. ANOVA yij = µ + τi + ε factor: cuantitativo ε=y–ŷ Objetivo OLS: Minimizar: ε’*ε (SSE) ε = vector de residuales ∂ε’*ε = 0 ∂β1 b^ = (X’X)-1X’y b^ = estimadores de los coeficientes y = vector de observaciones ♥X = la matriz de diseño • 1 fila por cada observación • 1 columna por cada coeficiente estimado Ejemplo: A Bajo B y= Alto 25 26 31 34 23 20 27 22 Bajo 25 26 23 20 Alto 31 34 27 22 Modelos: y = β0 + β1xA + ε y = β0 + β2xB + ε y = β0 + β1xA + β2xB + ε y = β0 + β1xA + β2xB + β3 xA xB + ε … etc.