3.3 determinantes
Anuncio

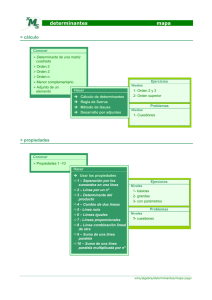
Bloque 3: 3.3 DETERMINANTES Programa: 1.- Definición inductiva de determinante de una matriz. Determinantes 2x2 y 3x3. Menor complementario. Adjunto o cofactor de un elemento. Teorema fundamental. Ejemplos. Determinante de matrices triangulares. 2.- Propiedades de los determinantes. 3.- Determinantes y matriz inversa. Determinantes y rango. Bibliografía.Grossmann (cap II) J. de Burgos (cap IV) ------------------------ 1.- Definición inductiva de determinante de una matriz. Determinantes 2x2 y 3x3. Menor complementario. Adjunto o cofactor de un elemento. Teorema fundamental. Ejemplos. Determinante de matrices triangulares. Si ⎡ a11 A=⎢ ⎣a21 ⎡ a11 Si A = ⎢ a ⎢ 21 ⎢⎣ a 31 a12 ⎤ a22 ⎥⎦ entonces se define det(A)=|A|=a11 a22 - a12 a21 . a13 ⎤ a 22 ⎥ a 23 ⎥ se define det(A)=|A| = a11 a 32 a 33 ⎥⎦ a12 a 22 a 32 a 23 a 33 − a12 a 21 a 23 a 31 a 33 + a13 a 21 a 22 a 31 a 33 . Se puede expresar |A|=a11a22a33+.a21a32a13+ a12 a23 a31 - a13 a22 a31 - a12 a21 a33 - a11 a23 a33. + ; o bien . Definición.- Menor complementario Mij Definición.- Cofactor o adjunto de un elemento aij A ij = (-1)i+j M i j Definición de determinante de una matriz .n |A| = ∑a j =1 ij Aij TEOREMA FUNDAMENTAL n n n j=1 i=1 j =1 |A|= ∑ a 1 j A 1 j = ∑ a i j Aij = ∑ aij Aij (fila 1) (fila i) (Demostración en Grossman página 141). (columna j) 2.- Propiedades de los determinantes 1.- Si una fila (o columna) es 0 → |A|=0 2.- Si se multiplica por k una fila del det(A) → det(kA)=kdet(A) 3.- Si f iA + fiB =fiC y todas las demas filas iguales entonces → |C|=|A|+|B| 4.- Si se permuta las filas fi y fj → |A| cambia de signo 5.- Si fi=fj →|A|=0 6.- Si fiA = α fjA → |A| = 0 7.- Si se hace la operación elemental fiA+ α fjA entonces |A| no cambia. En general si a fiA se le suma combinación lineal de otras filas entonces | A| permanece invariable. fqg Algebra Lineal EII 08-09 1/2 3.- Determinantes y matriz inversa. Determinantes y rango. TEOREMA: |A|=0 ⇔ vectores filas son linealmente dependientes. n Propiedad: Σ fila por los adjuntos de otra fila paralela es 0 ⇔ ∑a k =1 TEOREMA: |A|=|At| . ik A jk = 0 TEOREMA: |AB| = |A| . |B| (La demostración se basa en los lemas 1 y 2) Lema 1: Determinantes de las matrices elementales |Ef i j |= -1. |E fα i| = α. |Efi+α j| = 1 Siendo E cualquier matriz elemental. Lema 2 : |E . B| = |E| . |B| Lema 3 : A es regular ⇔ |A|≠0 Definición de matriz adjunta Aadj. Propiedad |Aadj| = |A|n-1 Cálculo de la inversa de una matriz: A-1 = 1 t A A adj Teorema Creciente.Son equivalentes las cinco proposiciones siguientes: 1) A es regular 2) AX = 0 solo tiene la solución trivial x = 0 . 3) AX = b tiene una única solución. 4) A ∼ I 5) A = producto de matrices elementales. 6) |A| ≠ 0. ------------------------------ Bloque 4.- SISTEMAS DE ECUACIONES LINEALES. 1.- Sistemas de ecuaciones lineales (SEL). Definiciones y propiedades. 2.- Sistemas de Cramer. Regla de Cramer. 3.- Teorema de Rouché-Frobenius. SEL Homogéneos. 4.- Método de Gauss. Bibliografía .“Algebra lineal” J. de Burgos. McGraw Hill. “Algebra lineal y Geometría” López-Pellicer y García García. “Lecciones de Algebra lineal” J.L.Pinilla “Problemas de Algebra” A. de la Villa. “Problemas de Algebra lineal” J.L.Pinilla. “Problemas de Algebra lineal” Tebar Flores. fqg Algebra Lineal EII 08-09 2/2