Nociones básicas de convexidad

Pontificia Universidad Católica
Escuela de Ingeniería
Departamento de Ingeniería Industrial y de Sistemas
Clase 8 • Nociones Básicas de Convexidad
ICS 1102 • Optimización
Profesor : Claudio Seebach
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 91
Función Cuasi-Convexa
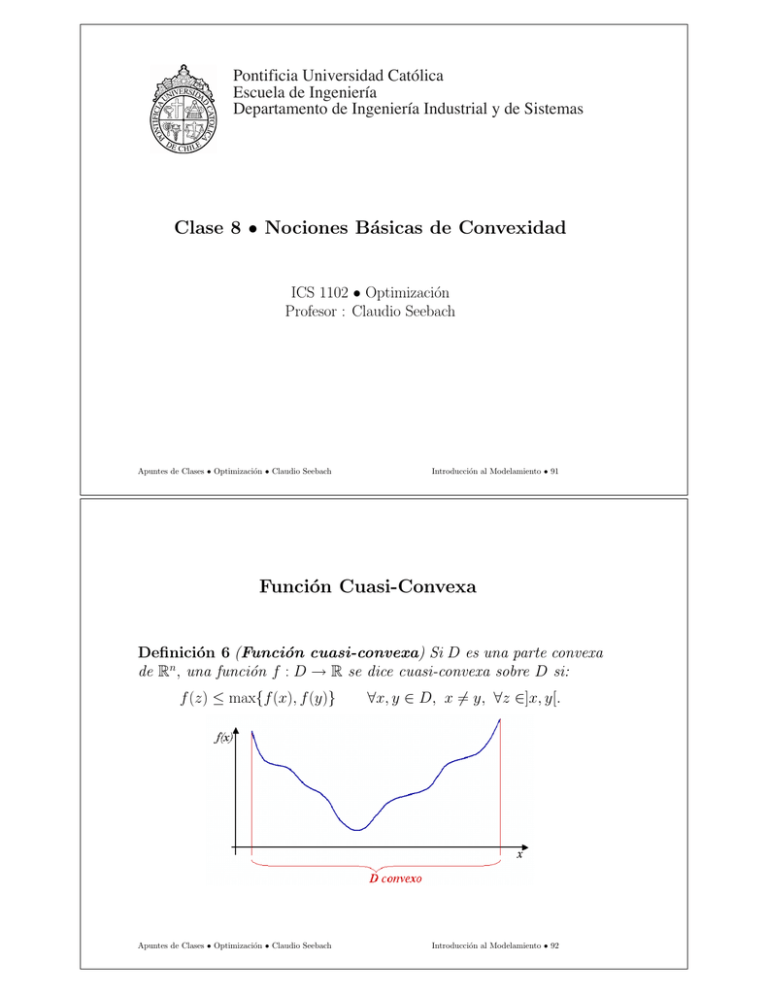
Definición 6 (Función cuasi-convexa) Si D es una parte convexa
de Rn, una función f : D → R se dice cuasi-convexa sobre D si:
f (z) ≤ max{f (x), f (y)}
Apuntes de Clases • Optimización • Claudio Seebach
∀x, y ∈ D, x %= y, ∀z ∈]x, y[.
Introducción al Modelamiento • 92
Funciones Convexas
• Las funciones convexas presentan favorables propiedades al optimizar.
Por ejemplo, un punto mı́nimo local es siempre mı́nimo global.
!"# $%&'()&*# ')&+*,"# -.*#*&/"& $"+)."01*# -.)-(*2"2*# "1 )-/(3(4".5 6). *7*3-1)8 %& -%&/)
•39&(3)
Sin
embargo
no necesariamente este óptimo será único. Por ejemplo la
1)'"1 *# #(*3-.* 39&(3) :1)0"15 ;(& *30".:) &) &*'*#".("3*&/* *#/* <-/(3) #*.= >&(')5
función
en !la!""figura
tiene@Avarias
soluciones
6).
*7*3-1) f
1" (x)
$%&'(<&
*& 1" ?(:%."
/(*&* +".("#
#)1%'()&*#óptimas.
<-/(3"#5
"#$%
!
!"#$%#&"'()'*"+%,-"#)*'./&-01*
• Ası́, surge la necesidad de definir las funciones estrictamente convexas.
?(:%.* @AB C7*3-1) 2* 3>1/(-1*# #)1%'()&*# <-/(3"#
D#98 #%.:* 1" &*'*#(2"2 2* 2*!&(. 1"# $%&'()&*# *#/.('/"3*&/* ')&+*,"#5
!"!#$%$&# ' !!"#$%&# '()*%$)+,'#)' $-#.'/+" #$% ! !""
# # ! !$ &'( # &'()$*'+ ,(-'(&$./
Introducción al Modelamiento • 93
! !"" $. $.-01&-%2$(-$ &'()$*% .'30$ # .14
Apuntes de Clases • Optimización • Claudio Seebach
! !!$ " !""! % !"" "" % !$ " !"! !"! " % !! !"" "
#"! $ "" $ #$ ! $ &'$ $( &
C# 2*'(. /)2" $%&'(<& *#/.('/"3*&/* ')&+*," *# /"30(E& ')&+*,"5 C& $).3" "&=1):" #* 2*!&*&
1"# $%&'()&*# *#/.('/"3*&/* '<&'"+"#5
!" ?(:%." @F" -.*#*&/" %&" &%*+" $%&'(<& ')&+*,"8 -*.) &) *#/.('/"5 G"0* 3*&'()&". H%*
/)2" $%&'(<& 1(&*"1 ! !"" ) '" % ( *# '<&'"+" I ')&+*," " 1" +*48 -*.) &( *#/.('/"3*&/* '<&'"+" &(
*#/.('/"3*&/* ')&+*,"5 6). )/." -"./*8 1" ?(:%." @F0 3%*#/." %&" $%&'(<& H%* &) *# &( '<&'"+" &(
')&+*,"8 -*.) H%* 1)'"13*&/* '*.'" 2* "! *# '<&'"+" I 1)'"13*&/* '*.'" 2* "" *# ')&+*,"5
Funciones Estrictamente Convexas
"#$%
"#$%
Definición 7 (Función estrictamente convexa) Sea f (x) : D →
R, con D convexo. Entonces, f (x) es estrictamente convexa sobre D
si:
f ((1 − λ)x1 + λx2)) < (1 − λ)f (x1)$ + λf (x2)
!"#
$&
∀x1, x2$'∈ D, λ ∈ [0, 1] .
!$#
?(:%.* @FB G"#)# *#-*'("1*# 2* $%&'()&*#
D ')&/(&%"'(<& #* 2*3)#/.".= H%* #( ! !"" *# ')&+*,"8 *&/)&'*# *1 1%:". :*)3E/.(') 2* 1)# -%&/)#
H%* #"/(#$"'* ! !"" ! " 2*0* ')&#/(/%(. %& ')&7&/) ')&+*,) -"." '%"1H%(*. "
()*+*,$%$&# - #1 # # # ! !$ # % !! $ # &'()$*'/ # &'()$*%/ $(-'(&$. 5'. &'(67(-'. 8$ (1)$5
)! !#" ) "" $ #*#!"" ! "# .'( &'()$*'. #" $ ! &
@J
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 94
!"!#$%$&# ' !!"#$%&# '()*%$)+,'#)' $-#.'/+" #$% ! !"" # # ! !$ &'( # &'()$*'+ ,(-'(&$./
! !"" $. $.-01&-%2$(-$ &'()$*% .'30$ # .14
! !!$ " !""! % !"" "" % !$ " !"! !"! " % !! !"" "
#"! $ "" $ #$ ! $ &'$ $( &
C# 2*'(. /)2" $%&'(<& *#/.('/"3*&/* ')&+*," *# /"30(E& ')&+*,"5 C& $).3" "&=1):" #* 2*!&*&
1"# $%&'()&*# *#/.('/"3*&/* '<&'"+"#5
!" ?(:%." @F" -.*#*&/" %&" &%*+" $%&'(<& ')&+*,"8 -*.) &) *#/.('/"5 G"0* 3*&'()&". H%*
Casos Especiales
/)2" $%&'(<& 1(&*"1 ! !"" ) '" % ( *# '<&'"+" I ')&+*," " 1" +*48 -*.) &( *#/.('/"3*&/* '<&'"+" &(
*#/.('/"3*&/* ')&+*,"5 6). )/." -"./*8 1" ?(:%." @F0 3%*#/." %&" $%&'(<& H%* &) *# &( '<&'"+" &(
')&+*,"8 -*.) H%* 1)'"13*&/* '*.'" 2* "! *# '<&'"+" I 1)'"13*&/* '*.'" 2* "" *# ')&+*,"5
"#$%
"#$%
$
$&
$'
!$#
!"#
• (a) : Toda función
lineal
(x) =*#-*'("1*#
ax + b 2*
es $%&'()&*#
cóncava y convexa a la vez,
?(:%.*
@FB fG"#)#
pero ni estrictamente cóncava ni estrictamente convexa.
D ')&/(&%"'(<& #* 2*3)#/.".= H%* #( ! !"" *# ')&+*,"8 *&/)&'*# *1 1%:". :*)3E/.(') 2* 1)# -%&/)#
• (b) !: !""
La!función
localmente
cerca ')&+*,)
de x1 es-"."
cóncava
y localmente
cerca
H%* #"/(#$"'*
" 2*0* ')&#/(/%(.
%& ')&7&/)
'%"1H%(*.
"
de x2 es convexa.
()*+*,$%$&# - #1 # # # ! !$ # % !! $ # &'()$*'/ # &'()$*%/ $(-'(&$. 5'. &'(67(-'. 8$ (1)$5
)! !#" ) "" $ #*#!"" ! "# .'( &'()$*'. #" $ ! &
@J
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 95
Criterios prácticos de convexidad de funciones
• Sea f (x) = f (x1, x2, ..., xn) continua y dos veces diferenciable.
• Su matriz Hessiana será:




H=


∂ 2f
∂ 2f
2
∂x1 ∂x2
∂x1
∂ 2f
∂ 2f
∂x2 ∂x1
∂x22
..
∂ 2f
∂xn ∂x1
• Esta matriz es simétrica. ¿por qué?
Apuntes de Clases • Optimización • Claudio Seebach
...
∂ 2f
∂x1 ∂xn
...
∂ 2f
∂x2n







Introducción al Modelamiento • 96
Caracterización de la matriz Hessiana
• Matrices menores de una matriz:
• Los determinantes de las matrices menores se denominan ∆i.
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 97
Caracterización de la matriz Hessiana
Definición 8 Caracterización de la matriz Hessiana
1. Si ∆i > 0 ∀i ⇒ H es definida positiva.
# T H d# > 0.
Para cualquier vector d# en Rn se cumple que (d)
2. Si ∆i ≥ 0 ∀i ⇒ H es semidefinida positiva.
# T H d# ≥ 0.
Para cualquier vector d# en Rn se cumple que (d)
3. Si ∆i < 0 ∀i impar y ∆i > 0 ∀i par. (i.e. ∆1 < 0, ∆2 > 0,
∆3 < 0, ...,) ⇒ H es definida negativa.
Para cualquier vector d en Rn se cumple que dT Hd < 0.
4. Si ∆i ≤ 0 ∀i impar y ∆i ≥ 0 ∀i par. (i.e. ∆1 ≤ 0, ∆2 ≥ 0,
∆3 ≤ 0, ...,) ⇒ H es semidefinida negativa.
Para cualquier vector d en Rn se cumple que dT Hd ≤ 0.
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 98
Caracterización de una Función Convexa
Definición 9
• Sea f (#x) dos veces diferenciable sobre D, con D ∈ Rn y convexo.
• Entonces f (#x) es convexa sobre D si y solo si D2f (x) = H es
semidefinida positiva ∀x ∈ D.
• Equivalentemente: dT D2f (x)d ≥ 0, ∀d ∈ Rn, ∀x ∈ D.
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 99
Caracterización de una función convexa
Ejemplo: Sea f (x1, x2) = 2x1 − 3x2 + x41 + x1x2 + x22. Las derivadas parciales son:
∂f
= 2 + 4x31 + x2
∂x1
∂f
= −3 + x1 + 2x2
∂x2
y las segundas derivadas serı́an:
∂ 2f
= 12x21
∂x21
∂ 2f
=1
∂x1∂x2
De esta forma, la matriz Hessiana es:
H=
'
∂ 2f
=1
∂x2∂x1
∂ 2f
= 2.
∂x22
(
12x21 1
.
1 2
Los determinantes menores son ∆1 = 12x21, no negativo para todo )
punto del dominio, y
1
1
2
2
.
∆2 = 24x1 − 1. Pero, ¿∆2 ≥ 0? Sólo si x1 ≥ 24 , es decir, si |x1| ≥ 24
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 100
!!!
! "#"!"
!"!"
!!!
!"
!"" !"!
!!!
!"
!"! !""
!!!
! ##
!"!!
!
"#"!" "
$!
#
" función
#
Caracterización de una
convexa
/% %$0# 12*3#4 "# 3#0*+5 6%$$+#(# %$.
72$ )%0%*3+(#(0%$ 3%(2*%$ $2( !" ! "#"!" % (2 (%&#0+,2 8#*#
" 02)2 8'(02 )%" )23+(+24 ! !! !
"
"
!
!
#$"" ! "# 9%*24 :!! " %; <="2 $+ "" " !# % %$ )%>+*4 $+ !"" ! " !#
#?$-4 ! &"' %$ >2(,%@# $2A*% 02)2
• f (x) es convexa sobre todo dominio convexo construido en la región achurada:
"!
!
!
!
#
!"
"#
#
!"
• f (x) no es convexa sobre toda la región achurada, ya que esta región no es convexa.
B+&'*% CD. /23+(+2 )% ! &"" % "! '
)23+(+2 >2(,%@2 >2($0*'+)2 %( "# *%&+=( #>E'*#)# )% "# B+&'*# CDF
G$ +382*0#(0% )%$0#>#* H'% ! &"' (2 %$ >2(,%@# $2A*% 02)# "# *%&+=( #>E'*#)# %( "# B+&'*# CD4 !#
H'% %$0# *%&+=( (2 %$ >2(,%@#F ?$+3+$324 A#$0# H'% "# 1'(>+=(
)%!(#
$ $2A*% '( )23+(+2 >2(,%@2
# " $% "
H'% +(>"'!# #"&'(# *%&+=( (2 #>E'*#)# I#"&J( 8'(02 %( !
>2(,%@# 8'%$ %" 6%$$+#(2 (2 $%*-# $%3+)%!(+)2 82$+0+,2KF
Apuntes de Clases • Optimización • Claudio Seebach
"
!# %
"
!#
8#*# H'% "# 1'(>+=( (2 $%#
Introducción al Modelamiento • 101
!"#$#%&'&() *+ !" & #$ %&' (')*# +,&-#.' /# !! 0 &! ! &"' #$ /#!&"/' (,$"*"-'1 #$ /#+")1 '" &! ! &"'' (
%% #' $ !! % ' "! %% #&*,&+#$ ! &"' #$ #$*)"+*'2#&*# +,&-#.' $,3)# &#
G( %" %L%38"2 #(0%*+2*4 ! &' %$ %$0*+>0#3%(0% >2(,%@# $2A*% 02)# *%&+=( >2(,%@# >2(0%(+)# %(
"# *%&+=( "" ) "!"
2 %( "# *%&+=( "" ( ""!# ( "! $ !# G$0#$ *%&+2(%$ %@>"'!%( %@8"->+0#3%(0% # "2$
!#
8'(02$ %( H'% "" !
!"
"
!#
= "" !
""
!#
I,%* B+&'*# CMKF
Caracterización de una función convexa
"!
!
!
Proposición 9 Si D es una parte convexa de Rn y D2f (x) es definida
"# f (x) es
#
positiva, es decir, dT D2!f (x)d
> 0, ∀d ∈ Rn, d# %= 0, entonces
!"
!"
estrictamente convexa sobre D.
• Importante, la relación es causal:
Si el Hessiano es definido positivo ⇒ la función es estrictamente convexa
CM. /23+(+2 (2 >2(,%@2 )% ! &"" % "! '
Si la función esB+&'*%
estrictamente
convexa ! el Hessiano es definido positivo
G$ +382*0#(0%
)%$0#>#* "# >#'$#"+)#) )% %$0# 8*282$+>+=(. $+ %" 6%$$+#(2 %$ )%!(+)2 82$+0+,24
• Ejemplo:
%(02(>%$ "# 1'(>+=(
>2(,%@#4
8%*2 (2D#"
&"' %$ %$0*+>0#3%(0%
4
2 *%,N$F G$ )%>+*4
f (x) =%$x%$0*+>0#3%(0%
es estrictamente
convexa,
f (x) = 12x2 no $+es! definida
positiva en x = 0.
Apuntes de Clases • Optimización • Claudio Seebach
OP
Introducción al Modelamiento • 102
Ejercicios resueltos
• Considere el siguiente problema de optimización:
P)
s.a
min x2 + y 2 + z 2 − 6000(x + y + z)
x + 2y + 4z ≤ 4000
x, y, z ≥ 0
• Función objetivo cuadrática, estrictamente convexa. Su matriz Hessiana:


2 0 0
D2f (x, y, z) =  0 2 0  = H
0 0 2
• H es definida positiva ⇒ f (x, y, z) es estrictamente convexa.
• D es un dominio acotado, cerrado y no vacı́o ⇒ P ) admite solución óptima.
• D es convexo y f (·) es estrictamente convexa ⇒ P ) admite solución óptima única.
Apuntes de Clases • Optimización • Claudio Seebach
Introducción al Modelamiento • 103