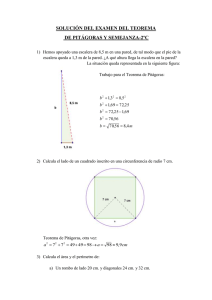
No importa la letra Escuela: Prof. (a): Curso:
Anuncio

No importa la letra Plan de clase (1/3) Escuela: ______________________________________ Fecha: _________ Prof. (a): _______________________________________________________ Curso: Matemáticas 3 Secundaria Eje temático: FEM Contenido: 9.2.5 Explicitación y uso del Teorema de Pitágoras. Intención didáctica: Que los alumnos expresen algebraicamente las relaciones entre los cuadrados de los lados de triángulos rectángulos. Consigna. Reunidos con dos compañeros, realicen lo que se indica enseguida: 1. Expresen algebraicamente los valores solicitados en función de las otras dos variables. a c z y a c b a x Figura 1 Figura 2 Figura 3 z 2 __________ ______ c 2 __________ ______ c 2 __________ ______ x 2 __________ ______ a 2 __________ ______ a 2 __________ ______ y 2 __________ ______ 2a 2 __________ ______ b 2 __________ ______ z __________ ______ c __________ ______ a __________ ______ x __________ ______ a __________ ______ b __________ ______ y __________ ______ 2. c __________ ______ ¿Cuál es la expresión algebraica que representa el teorema de Pitágoras en cada figura y que se enuncia a continuación? “En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”. Figura 1: _____________ Figura 2: _____________ Figura 3: _____________ Consideraciones previas: En los planes de clase del contenido 9.2.4, los alumnos realizaron varias actividades que implicaron determinar las relaciones entre las áreas de los cuadrados construidos sobre los lados de un triángulo rectángulo y concluyeron que “la suma de las áreas de los cuadrados construidos con las medidas de los lados menores es igual al área del cuadrado construido con la medida del lado mayor”. Esta propiedad es exclusiva de los triángulos rectángulos y recibe el nombre de Teorema de Pitágoras. En este momento tendrán que simbolizar esta propiedad y las relaciones que se desprenden de ella. Con respecto a la primera actividad, es probable que algunos alumnos tengan dificultad para escribir las expresiones algebraicas solicitadas; si esto ocurre, se les pueden plantear preguntas de reflexión sobre los significados de cada expresión, por ejemplo, para el primer caso: Si se construye un cuadrado que tenga por lado la hipotenusa representada como z, ¿qué representa z2? ¿Qué representa x2? ¿Y y2? ¿A qué equivale z2? Con ello, se espera que los alumnos puedan reconocer que z2 representa el área del cuadrado sobre la hipotenusa; por lo que z2 equivale a x2 + y2. Una vez que los alumnos logren establecer la igualdad z2 = x2 + y2, se espera que no haya dificultad en escribir las relaciones restantes, ya que sólo implica realizar despejes de la relación z2 = x2 + y2. Con respecto a la segunda actividad, es probable que para la figura 2, los alumnos digan que hay un error, es decir, que un cateto del triángulo rectángulo isósceles debe asignarse con otra letra. Si esto ocurre, es conveniente aclarar que se usa la misma letra o literal (a) porque los dos catetos son iguales. En este caso, se espera que los alumnos escriban cualquiera de las dos expresiones algebraicas siguientes: c2 = a2 + a2 c2 = 2a2 Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? __________________________________________________________ __________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? __________________________________________________________ __________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Seguimos con Pitágoras Plan de clase (2/3) Escuela: ____________________________________ Fecha:__________ Prof. (a): ______________________________________________________ Curso: Matemáticas 3 Secundaria Eje temático: FEM Contenido: 9.2.5 Explicitación y uso del Teorema de Pitágoras. Intención didáctica: Que los alumnos apliquen el teorema de Pitágoras para resolver problemas. Consigna: Organizados en equipos, resuelvan los siguientes problemas, pueden utilizar calculadora. 1. Un albañil apoya una escalera de 5 m de largo contra un muro vertical. El pie de la escalera está a 2 m del muro. Calculen a qué altura se encuentra la parte superior de la escalera. 2. En la esquina de una plaza rectangular se encuentra un puesto de helados. Si estoy en la esquina opuesta diagonalmente, ¿cuántos metros tengo que recorrer sobre la diagonal para llegar al puesto? Los lados de la plaza miden 48 m y 64 m. 3. ¿Cuál es la máxima distancia que puedes recorrer sin cambiar de dirección en una pista de patinaje en forma de rombo, si cada lado mide 26 m y la diagonal menor 40 m? 4. El pueblo B está en línea recta 40 km al norte del pueblo A y el pueblo C está, en línea recta, 30 km al este de B. ¿Cuál es la distancia entre los pueblos A y C? Consideraciones previas: En los problemas anteriores será muy común encontrar que los alumnos dibujen la situación para ayudarse a comprenderla, sin embargo, en la puesta en común se pueden compartir las diversas estrategias aplicadas. En todos los casos, es pertinente utilizar el teorema de Pitágoras para encontrar la respuesta. Con respecto al problema 4, es probable que los alumnos no sepan interpretar adecuadamente el problema. Si sucediera que nadie en el grupo hace una clara interpretación de las posiciones de A, B y C, será necesario orientarlos al respecto a través de preguntas como: ¿cuál es el primer punto que debemos ubicar? ¿Dónde está el siguiente pueblo (B)?, etc., incluso se les puede pedir que justifiquen sus respuestas. Una vez hecho un dibujo semejante al de abajo, se les dejará buscar la manera de responder la pregunta del problema. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? __________________________________________________________ __________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? __________________________________________________________ __________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Se parecen Plan de clase (3/3) Escuela: ___________________________________ Fecha: _________ Prof. (a): _______________________________________________________ Curso: Matemáticas 3 Secundaria Eje temático: FEM Contenido: 9.2.5 Explicitación y uso del Teorema de Pitágoras. Intención didáctica: Que los alumnos usen el Teorema de Pitágoras y las propiedades de figuras semejantes para resolver problemas. Consigna: Los dos triángulos que aparecen abajo son semejantes. Individualmente, calculen el perímetro de cada uno. z 60 cm 2 y 1 32 cm 8 cm x Consideraciones previas: Para resolver este problema no basta aplicar el teorema de Pitágoras, sino que es necesario recordar y aplicar las propiedades de los triángulos semejantes. Para llegar a la respuesta existen varios caminos, por ejemplo, es probable que algunos alumnos se les ocurra primero determinar el valor de x por teorema de Pitágoras, luego, por semejanza determinar el valor de z, para finalmente determinar por semejanza o por Pitágoras el valor de y. Es importante, mientras los alumnos trabajan, observar si han quedado claros los dos conceptos o si hay dificultad en alguno de ellos. Si el tiempo lo permite se puede pedir al grupo que resuelva los siguientes problemas, si no, se pueden dejar de tarea y revisar sus procedimientos en una puesta en común en la siguiente clase. 1. En la siguiente figura los triángulos son semejantes. Calcula la longitud x y determina la distancia entre los puntos A y B. A x 64 cm 144 cm 48 cm B 2. Calcular el área de un hexágono regular si se sabe que la longitud de cada uno de sus lados mide 4 m. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? __________________________________________________________ __________________________________________________________ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? __________________________________________________________ __________________________________________________________ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre 14/15