Solución Del Examen Del Teorema De Pitágoras Y - Wiki 2010-11

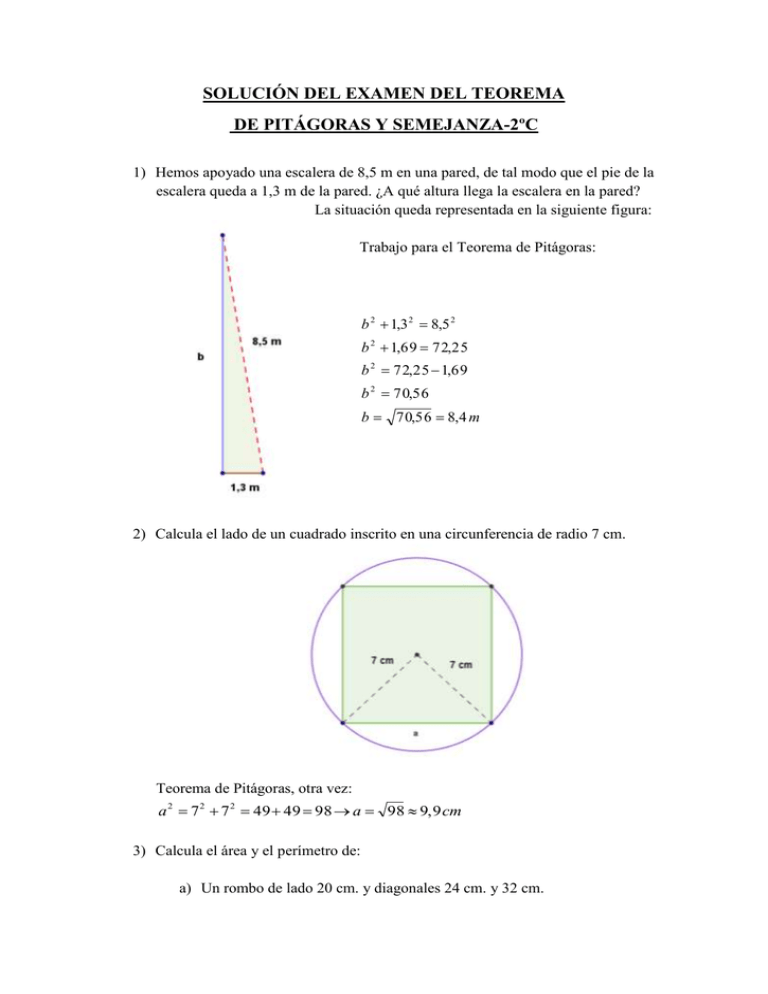
SOLUCIÓN DEL EXAMEN DEL TEOREMA
DE PITÁGORAS Y SEMEJANZA-2ºC
1) Hemos apoyado una escalera de 8,5 m en una pared, de tal modo que el pie de la
escalera queda a 1,3 m de la pared. ¿A qué altura llega la escalera en la pared?
La situación queda representada en la siguiente figura:
Trabajo para el Teorema de Pitágoras:
b 2  1,3 2  8,5 2
b 2  1,69  72,25
b 2  72,25  1,69
b 2  70,56
b  70,56  8,4 m
2) Calcula el lado de un cuadrado inscrito en una circunferencia de radio 7 cm.
Teorema de Pitágoras, otra vez:
a 2  7 2  7 2  49  49  98  a  98  9, 9 cm
3) Calcula el área y el perímetro de:
a) Un rombo de lado 20 cm. y diagonales 24 cm. y 32 cm.
No tenemos que pensar demasiado:
P  4 ·20  80 cm
D ·d 32·24
A

 384cm 2
2
2
b) Un trapecio isósceles de bases 5 cm. y 10 cm., y altura 4 cm.
Podemos calcular ya el área del trapecio:
Bb
10  5
A
·h 
·4  30 cm 2
2
2
Pero para calcular el perímetro necesitamos el valor de los lados iguales
laterales. Usamos el Teorema de Pitágoras, teniendo en cuenta que el
cateto menor mide 2,5 cm (pues es (10-5):2):
a 2  42  2, 52  16  6, 25  22,25  a  22,25  4, 7 cm
Así que el perímetro es: P  10  5  2 ·4,7  24, 4cm
c) Un hexágono regular de lado 10 cm.
P  6 ·10  60cm
Para calcular el área necesitamos el valor de la apotema (en caso de no
querer aplicar la fórmula, podemos simplemente calcular el área de uno
de los triángulos y multiplicar ese valor por 6, que por cierto es el origen
de la fórmula):
Utilizamos el Teorema de Pitágoras (one more time):
ap2  102  52  100 25  75  ap  75  8,7 cm
Y calculamos el área:
P ·ap 60 ·8,7
A

 30 ·8,7  261 cm 2
2
2
4) Calcula las siguientes áreas sombreadas:
a) Una flecha dentro de un cuadrado de lado 20 cm.
El modo más rápido es el siguiente: el área de la flecha es la diferencia
entre las áreas de dos triángulos:
El primero de los triángulos tiene base 20 cm. y altura 20 cm., y el
segundo tiene la misma base y altura 10 cm., con lo que el área de la
flecha es:
20 ·20 20 ·10

 200  100  100 cm 2
2
2
b) La superficie determinada por un cuadrante de circunferencia dentro de
un cuadrado de lado 20 cm.(la circunferencia pasa por el centro del
cuadrado)
A
Hay que tener cuidado con el radio del cuadrante de círculo, que no es la
mitad del lado del cuadrado, sino la mitad de su diagonal. Para calcular
su valor, usamos el Teorema de Pitágoras:
r 2  102  102  100 100  200  r  200  14,1cm
Y el área solicitada es:
 ·14,12
 ·200
A  202 
 400 
 400  50  242, 9 cm 2
4
4
5) A una hora determinada de la mañana, un edificio de 20 metros de altura
proyecta una sombra de 25 metros. ¿Cuál es la altura de un árbol cercano que
proyecta una sombra de 7,5 metros?
Las sombras y las alturas son proporcionales, así que, llamando x a la altura del
árbol:
20·7,5
20
x

x
 20·0, 3  6 m
25 7, 5
25
6) Calcula la altura de la Torre de Hércules a partir de la información de la figura:
Este ejercicio es exactamente igual al anterior, con la única salvedad de que
tenemos que considerar como “sombra” de la Torre de Hércules:
80 ·17
17
x

x
 4 ·17  68 m
20 80
20