Cálculo Integral para primeros cursos universitarios
Anuncio

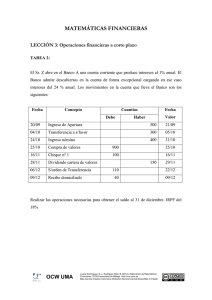
SÍMBOLOS
SIGNIFICADO
`
conjunto de los números naturales
]+
conjunto de los números enteros positivos o naturales
]
conjunto de los números enteros
]*
conjunto de los números enteros menos el cero
_
conjunto de los números racionales
R
conjunto de los números reales
R*
conjunto de los números reales menos el cero
R2
plano real
{a,b,…}
conjunto formado por a, b, …
∈
pertenece a
∉
no pertenece a
⇒
implica
⇔
doble implicación
/
tal que
∋
tal que
∀
para todo
∃
existe
⊂
contenido
∪
unión
Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es
∩
intersección
∅
conjunto vacío
→
tiende hacia
≠
distinto
≅
aproximadamente
≈
semejante
<
menor ….que
>
mayor ….que
≤
menor o igual… que
≥
mayor o igual … que
±
más menos
∓
menos más
⋅
producto
∞
infinito
[a, b]
intervalo cerrado
(a , b)
intervalo abierto
[a, b), (a , b]
intervalos semiabiertos, semicerrados
(a ,∞)
intervalo no acotado o semirrecta
[a, ∞)
semirrecta
x≥a
(−∞,a)
semirrecta
x<a
x>a
Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es
(−∞,a]
semirrecta
(−∞,∞)
expresa el conjunto de los números reales
x
valor absoluto de x
(x, y)
coordenadas cartesianas de un punto del plano
P (x, y )
punto P cuyas coordenadas en el plano son x e y
(x, y,z)
coordenadas cartesianas de un punto del espacio
P (x, y,z)
punto P cuyas coordenadas en el espacio son x, y y z
d(x, y )
distancia de x a y
ln x
logaritmo neperiano de x
loga x
logaritmo en base a de x
n!
factorial de
n
k
x≤a
n = n ⋅ (n − 1)⋅ (n − 2)…1
coeficiente binomial
n
n!
=
k k!(n− k)!
f : A→ R
función
Dom f
Dominio de
Im f
imagen de
g f
composición de funciones
f
R
con dominio en A y valores en
R
f
f
f
y
g
Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es
f −1
función inversa de
senx
seno de x
cos x
coseno de x
tagx
tangente de x
cot agx
cotangente de x
sec x
secante de x
cosecx
cosecante de x
arcsenx
arco seno de x
arccosx
arco coseno de x
arctagx
arco tangente de x
n→∞
n tiende hacia infinito
n→c
n tiende hacia “c”
lim f (x )
límite de
f (x ) cuando x tiende hacia “a”
lim f (x)
límite de
f (x ) cuando x tiende hacia infinito
lim f (x)
límite de
f (x ) cuando x tiende hacia “a” por la derecha
lim f (x)
límite de
f (x ) cuando x tiende hacia “a” por la izquierda
f ′(x)
derivada de
f ′(a )
derivada de f en el punto “a”
x→ a
x→∞
x→a
+
x→a −
f
f (x )
Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es
dy
dx
derivada de y respecto de x
f ′′(x )
derivada segunda de
f (x )
f ′′(a)
derivada segunda de f en el punto “a”
d2 y
dx
2
derivada segunda de y respecto de x dos veces
∫ f (x )dx
∫a f (x)dx
integral indefinida
b
[
]
F (x ) a
b
integral definida
F (b)− F (a)
aij
elemento de la fila i y columna j
I
matriz identidad
−1
A
matriz inversa de la matriz A
T
A
matriz traspuesta de la matriz A
det A = A
determinante de la matriz A
a
vector
G
por b
G
G
a por b
G
a
a⋅b
producto escalar de los vectores
a∧ b
producto vectorial de los vectores
Cálculo Integral para primeros cursos universitarios. Alejandre - Allueva, http://ocw.unizar.es