ECUACIONES BICUADRADAS. RESUELTOS
Anuncio
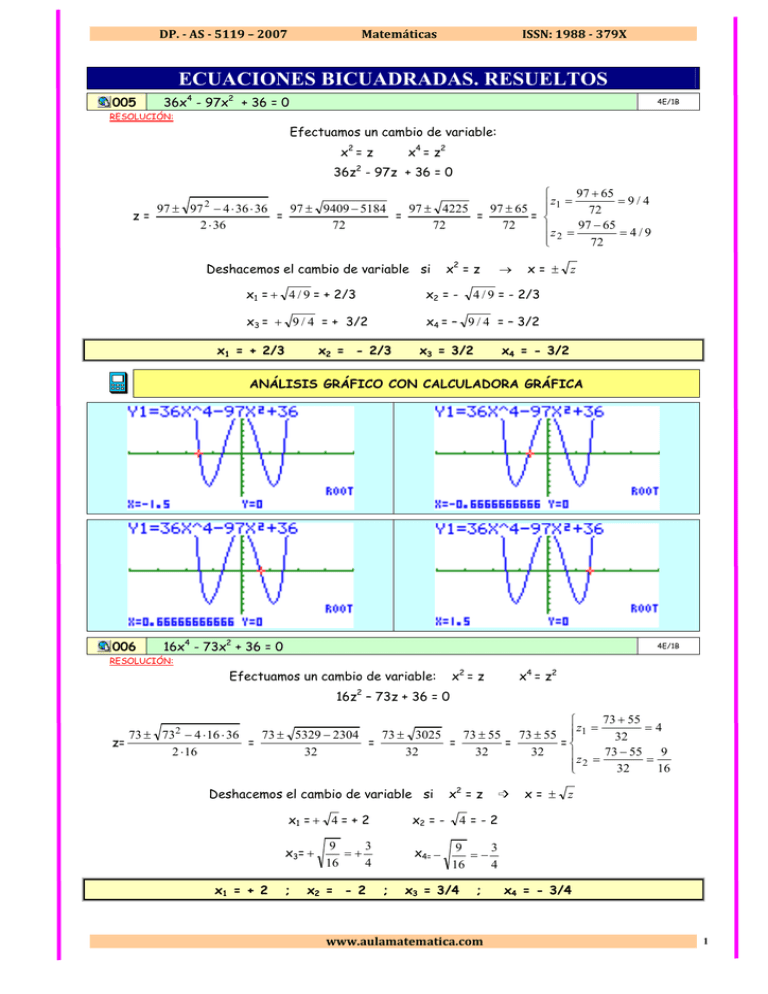
DP. - AS - 5119 – 2007 Matemáticas ISSN: 1988 - 379X ECUACIONES BICUADRADAS. RESUELTOS 005 36x4 - 97x2 + 36 = 0 4E/1B RESOLUCIÓN: Efectuamos un cambio de variable: x2 = z x4 = z2 36z2 - 97z + 36 = 0 97 + 65 z1 = =9/4 97 ± 97 − 4 ⋅ 36 ⋅ 36 97 ± 9409 − 5184 97 ± 4225 97 ± 65 72 z= = = = = 2 ⋅ 36 72 72 72 z = 97 − 65 = 4 / 9 2 72 2 Deshacemos el cambio de variable si x2 = z → x= ± z x1 = + 4 / 9 = + 2/3 x2 = - x3 = + 9 / 4 = + 3/2 x4 = – 9 / 4 = – 3/2 x1 = + 2/3 x2 = - 2/3 4 / 9 = - 2/3 x3 = 3/2 x4 = - 3/2 ANÁLISIS GRÁFICO CON CALCULADORA GRÁFICA 006 16x4 - 73x2 + 36 = 0 4E/1B RESOLUCIÓN: x2 = z Efectuamos un cambio de variable: x4 = z2 16z2 – 73z + 36 = 0 73 + 55 z = =4 73 ± 732 − 4 ⋅ 16 ⋅ 36 73 ± 5329 − 2304 73 ± 3025 73 ± 55 73 ± 55 1 32 z= = = = = = 2 ⋅ 16 32 32 32 32 z = 73 − 55 = 9 2 32 16 Deshacemos el cambio de variable si x1 = + 4 = + 2 x3 = + x1 = + 2 ; x2 = - 9 3 =+ 16 4 x2 = - 2 x2 = z x4= − ; ³ x= ± z 4=-2 9 3 =− 16 4 x3 = 3/4 ; www.aulamatematica.com x4 = - 3/4 1 Abel Martín 008 30 - x2 = 225 4E/1B x2 RESOLUCIÓN: mcm: x2 30x2 - x4 = 225 → - x4 + 30x2 - 225 = 0 x4 - 30x2 + 225 = 0 Se trata de un trinomio cuadrado perfecto: (x2 - 15)2 = 0 ♦ x2 - 15 = 0 x2 - 15 = 0 → x2 = 15 x=± x1 = + 15 ≅ 3.8729 15 ; x2 = - 15 ≅ - 3.8729 ¡¡OJO!! La calculadora gráfica tiene muchos problemas para encontrar los puntos de intersección de la gráfica con el eje OX en estos casos en los que dicho eje es tangente a la gráfica, por lo que tenemos que buscar métodos alternativos de visualización gráfica. 012 x4 + x2 + 1 = 0 4E/1B RESOLUCIÓN: Efectuamos un cambio de variable: x2 = z x4 = z2 z2 + z + 1 = 0 z= − 1 ± 12 − 4 ⋅ 1 ⋅ 1 2 ⋅1 = −1 ± 1 − 4 2 = −1 ± − 3 2 Como la raíz cuadrada de un número negativo no es un número real, podemos concluir que no hay ningún número Real que verifique la ecuación del enunciado. 2 Ecuaciones bicuadradas DP. - AS - 5119 – 2007 014 Matemáticas ISSN: 1988 - 379X x4 + x3 - 3x2 - 4x - 4 = 0 4E/1B RESOLUCIÓN: ¡¡¡ No se trata de una ecuación bicuadrada !!! Factorizamos por el método de Ruffini: 1 1 –2 –1 2 1 –2 1 2 1 –3 2 –1 2 1 –4 +2 –2 2 0 –4 +4 0 Seguimos por Ruffini pero no obtenemos ninguna raíz entera: (x + 2) (x – 2) (x2 + x + 1) = 0 x2 + x + 1 = 0 t= −b ± b 2 − 4 ⋅ a ⋅ c 2⋅a = − 1 ± 12 − 4 ⋅ 1 ⋅ 1 2 ⋅1 x1 = – 2 = −1 ± 1 − 4 2 = −1 ± − 3 2 ∉R x2 = 2 ANÁLISIS GRÁFICO CON CALCULADORA GRÁFICA 015 16x4 - 72x2 + 81 = 0 4E/1B RESOLUCIÓN: Se trata de un trinomio cuadrado perfecto: (4x2 - 9)2 = 0 [(2x + 3) (2x - 3)]2 = 0 (2x + 3)2 (2x - 3)2 = 0 ♦ 2x + 3 = 0 2x = - 3 x = - 3/2 x = - 1.5 ♦ 2x - 3 = 0 2x = 3 x1 = + 1.5 x = 3/2 ; x2 = - 1.5 ¡¡OJO!! La calculadora gráfica tiene muchos problemas para encontrar los puntos de intersección de la gráfica con el eje OX en estos casos en los que dicho eje es tangente a la gráfica, por lo que tenemos que buscar métodos alternativos de visualización gráfica. www.aulamatematica.com 3