Catedra Canciani
Anuncio
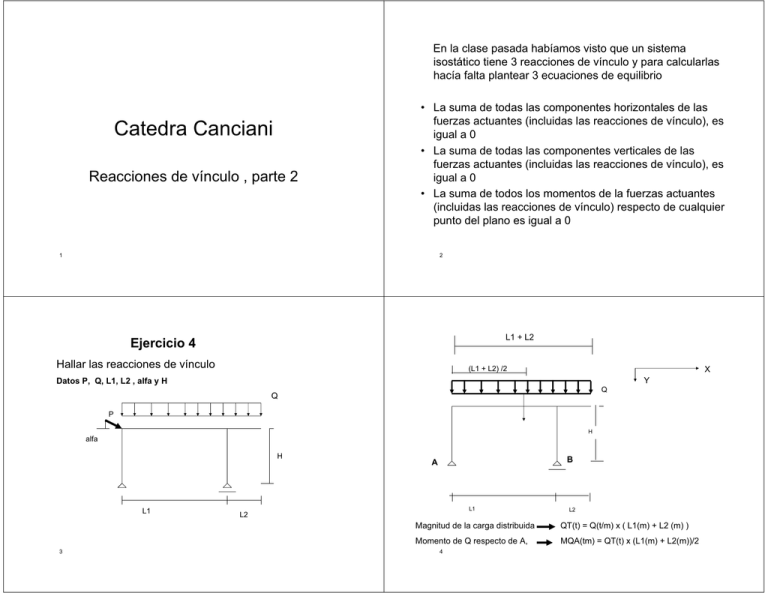
En la clase pasada habíamos visto que un sistema isostático tiene 3 reacciones de vínculo y para calcularlas hacía falta plantear 3 ecuaciones de equilibrio Catedra Canciani Reacciones de vínculo , parte 2 • La suma de todas las componentes horizontales de las fuerzas actuantes (incluidas las reacciones de vínculo), es igual a 0 • La suma de todas las componentes verticales de las fuerzas actuantes (incluidas las reacciones de vínculo), es igual a 0 • La suma de todos los momentos de la fuerzas actuantes (incluidas las reacciones de vínculo) respecto de cualquier punto del plano es igual a 0 1 2 L1 + L2 Ejercicio 4 Hallar las reacciones de vínculo (L1 + L2) /2 X Y Datos P, Q, L1, L2 , alfa y H Q Q P H alfa H L1 3 B A L1 L2 L2 Magnitud de la carga distribuida QT(t) = Q(t/m) x ( L1(m) + L2 (m) ) Momento de Q respecto de A, MQA(tm) = QT(t) x (L1(m) + L2(m))/2 4 Q P alfa X Y Py alfa P Px X Y Py Px Px(t) H H Py(t) FxA B A MPxA(tm) B A FyA QT(t) Fyb MQA(tm) L1 L2 L1 L2 Momento de reacción vinculo en B respecto de A MFyBA(tm) = FyB(t) x L1 (m) Px(t) = P(t) x cos alfa, Py(t) = P(t) x sen alfa x) Momento de Px respecto de A MPxA(tm) = Px(t) x H(m) 5 P Fxa Px(t) + FxA(t) = 0 MA) MPxA(tm) + MQA(tm) – FyB(t) x L1 (m)= 0 FyB y) FyA Py(t) + QT – FyA(t) – FyB(t)= 0 6 Q alfa X Py Y Py Px Px H Px = P x cos alfa 4m Y FxA FyA L1 B A FyA Fyb 5m L2 Px = 1,0 t x cos 45 ° Px = 0,71 t FxA B A X Py = P x sen alfa Fyb 2m Py = 1,0 t x sen 45 ° Py = 0,71 t Datos L1 = 5 m Magnitud de la carga distribuida QT(t) = 1,2 t/m x ( 5 m + 2 m) = 8,4 t L2 = 2m H =4m Momento de Q respecto de A, = 1,0 t Alfa 7= 45 ° MQA(tm) = QT(t) x (L1(m) + L2(m))/2 MQA(tm) = 8,41 t x ( 5m + 2m )/2 = 29,43 tm Q = 1,2 t/m P QT(t) = Q(t/m) x ( L1(m) + L2 (m) ) Momento de Px respecto de A 8 MPxA(tm) = Px(t) x H(m)= MPxA(tm) = 0,71 t x 4 m = 2,84 tm X y Py Px 4m FxA B A FyA Px = 0,71 t Py = 0,71 t QT(t) = 8,4 t MQA(tm) = Fyb 29,43 tm MPxA(tm) = x) 5m 2m Px(t) + FxA(t) = 0 0,71 t + FxA = 0 FxA = - 0, 71 t MA) MPxA + MQA - FyB x L1 = 0 2,84 tm + 29,43 tm – FyB x 5m = 0 y) 2,84 tm FyB = 6,45 t Py(t) + QT(t) – Fy(t) – FyB(t)= 0 0,71 t + 8,4 t – FyA(t) – FyB(t) = 0 FyA = 2.,662 t 9 10 Formas de representar cargas distribuidas en barras inclinadas Ejercicio N° 5 Lh Q Lh Datos Q, L1, L2 y H Hallar las reacciones de vínculo Q Q Li Li H Q total ( t ) = Q( t/m) x Lh( m ) 11 Q total ( t ) = Q( t/m) x Li( m ) 12 L1 L2 Q X L 1 + L2 X FxA Y A Y QT (L1 + L2)/2 FyA H QT(t) Q MQA(tm) A B QT H L2 L1 FyB B Momento de la reacción de vinculo en B respecto de A MFyBA(tm) = FyB(t) x (L1(m) + L2(m)) Magnitud de la carga distribuida Q X ) FxA = 0 FxA QT(t) = Q(t/m) x (L1(m) + L2(m)) MA ) MQA(tm) – FyB(t) x (L1(m) + L2(m))= 0 FyA Momento de la carga distribuida Q respecto de A Y ) QT(t) – FyA – FyB = 0 FyB 13 MQA(tm) 14 = QT(m) x (L1(m) + L2 (m))/2 Q Q X FxA A X FxA A QT Y Y FyA FyA H H Datos MQA(tm) L1 = 2 m B B L2 = 3 m L1 L2 FyB L2 L1 H=3m FyB Q = 1.100 Kg/m X) Magnitud de la carga distribuida Q QT(t) = Q(t/m) x (L1(m) + L2(m)) QT(t) = 1,1(t/m) x ( 2 m + 3 m ) = 5,5 t Momento de la carga distribuida Q respecto de A MQA(tm) = QT(m) x (L1(m) + L2 (m))/2 MQA(tm) = 5,5 t x ( 2 m + 3 m )/2 = 13,75 tm 15 FxA(t) = 0 MA ) MQA(tm) – FyB ( L1 + L2 ) = 0 13,75 tm - FyB (2 m + 3 m) = 0 FyB = 2,75 t Y ) QT(t) – FyA – FyB = 0 5,5 16 t – FyA – 2,75 t = 0 FyA = 2,75 t Grados de libertad C A B En esta estructura la pieza ACB, es monolítica, luego tiene 3 grados de libertad. Las articulaciones en A y B le restringen dos grados de libertad cada una, en total 4. Luego al tener más restricciones s que grados de libertad la estructura es hiperestática, o sea que no se puede resolver con las ecuaciones de la estática 17 18 C D E C B D E B A A En esta estructura la pieza ACDEB, es monolítica, luego tiene 3 grados de libertad. En esta estructura la pieza ACDEB, es monolítica, luego tiene 3 grados de libertad. Las articulaciones en A le restringe 2 grados de libertad, el apoyo móvil en B le restrige 1 grado de libertad, en total 3 Las articulaciones en A y B le restringen 2 grados de libertad cada una, en total 4 Luego al tener igual cantidad de restricciones s que grados de libertad la estructura es isostática o sea que se puede resolver con las ecuaciones de la estática Luego al tener mayor cantidad de restricciones que grados de libertad la estructura es hiperestática o sea que no se puede resolver con las ecuaciones de la estática 19 20 C G D E C D G E B B A A En esta estructura G es una articulación, la pieza ACG, tiene 3 grados de libertad y la pieza GDEB, es monolítica, luego tiene otros 3 grados de libertad, en total 6 Las articulaciones en A , B y C e restringen 2 grados de libertad cada una, en total 6 Luego al tener igual r cantidad de restricciones que grados de libertad la estructura es isostática o sea que se puede resolver con las ecuaciones de la estática En esta estructura G A es un empotramiento , la pieza ACG, tiene 3 grados de libertad y la pieza GDEB, otros 3, en total 6 El empotramiento en A le restringe 3 grados de libertad, las articulaciones en B y C 2 grados de libertad cada una, en total 7 Luego al tener mayor cantidad de restricciones que grados de libertad la estructura es hiperestàtica o sea que no se puede resolver con las ecuaciones de la estática 21 22 Arcos Triarticulados C G D E C H B A En este sistema G y H son articulaciones, la pieza ACG, tiene 3 grados de libertad , la pieza GDEH otros 3 y la pieza HB también 3, en total 9 Las articulaciones en A , B , G y H le restringen 2 grados de libertad cada una, en total 8 Luego al tener menor cantidad de restricciones que grados de libertad el sistema es un mecanismo o sea que se mueve, luego no puede usarse como estructura resistente de ninguna construcción 23 A B La barra AC tiene 3 grados de libertad. La barra CB tiene otros 3 grados de libertad, en total la estructura tiene 6 grados de libertad. Las articulaciones en A. C y B restringen cada una 2 grados de libertad y en conjunto 6 grados de libertad, luego al tener la estructura igual número de grados 24 de libertad que restricciones , la misma es isostática. • Cuando un sistema tiene mas restricciones que grados de libertad es un hiperestático, o sea que no se puede resolver con las ecuaciones de la estática • Cuando tiene igual cantidad de restricciones que grados de libertad es un isostático, o sea que se puede resolver con las ecuaciones de la estática • Cuando tiene menor cantidad de restricciones que grados de libertad es un mecanismo, o sea que se mueve, luego no puede usarse como estructura resistente de ninguna construcción 25





