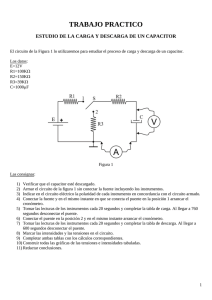
Problemas sobre Thevenin y circuitos RC (régimen transitorio)
Anuncio

Parcialito B (16/mayo/2012) En este parcialito tomaremos 2 problemas (o preguntas) : Una sobre el tema Teorema de Thevenin y/o Teorema de máxima trasferencia de potencia. El otro problema ( o pregunta) será sobre circuitos RC en régimen transitorio. El parcialito se tomará entre las 11:00 y las 12:00. Acá van algunos problemas tomados en parciales de años anteriores… Problemas sobre Thevenin y circuitos RC (régimen transitorio) 1)Hallar el circuito equivalente de Thévenin entre A y B para el siguiente circuito en el que todos los resistores son idénticos y las dos fuentes tiene igual f.e.m. (Especificar el criterio por el cual se determinan sus elementos. Desarrollar todos los cálculos. Si es necesario mostrar las transformaciones del circuito. Expresar la f.e.m y la resistencia del circuito equivalente en función de E y de R) 2) a) Determinar el equivalente de Thevenin del circuito de la figura, utilizando los siguientes datos: E1 = 125 V; E2 = 100 V; R1 = 20 ; R2 = 80 ; R3 = 24 (Redactar brevemente cuáles son los criterios para determinar los elementos que forman el circuito equivalente) b) Entre los puntos A y B se conecta una resistencia de carga RL. Calcular la potencia disipada en dicha resistencia cuando toma los valores RL = 10 y RL = 160 4) En el circuito de la figura la f.e.m de cada una de las fuentes es de 9 Volt, R1 = 20 , R2 = 60 y la resistencia de carga RL se puede variar desde 0 hasta 100 . a)¿Para qué valor de RL es máxima la potencia que se disipa en dicha resistencia de carga? ¿Cuánto vale esta potencia máxima? b) ¿Para qué valores de RL la potencia disipada en ella es el 75% de la máxima posible? 4) Dos baterías cuyas fuerzas electromotrices son E1 y E 2 y cuyas resistencias internas son R1 y R2 se conectan en paralelo entre los puntos a y b. Una resistencia variable R3 se conecta entre estos puntos. a)Demostrar que el conjunto de las dos baterías (red abierta entre a y b) se puede reemplazar por una f.e.m: E E1 R2 E2 R1 R1 R2 en serie con una resistencia R R1 R2 R1 R2 b) Inicialmente se ajusta el valor de R3 para que sea igual a R. Luego se va aumentando el valor de R3 . Entonces, ¿Cómo varían la intensidad de corriente por R3, la d.d.p entre a y b y la potencia disipada en R3? ¿Aumentan, disminuyen? EXPLICAR 2) Un capacitor de 5 mF, inicialmente descargado, se conecta a través de una resistencia de 500 con una batería 100 Volt. En el instante to = 0 se cierra la llave. a) Cuando han transcurrido 4 segundos calcular la energía que ha entregado la fuente, la que se ha almacenado en el capacitor y la que se ha disipado en la resistencia. b) Si en el circuito se intercala en serie un amperímetro ideal cuya menor división de la escala es 0,01 Ampere, estimar en cuánto tiempo, desde que se cerró la llave, se puede decir que la corriente es nula. Energía (Joules) 4) Un capacitor C = 1 mF, inicialmente descargado, se conecta a través de una resistencia R = 1 K con una batería cuya f.e.m es 100 Volt En el instante to = 0 se cierra la llave. a) Indicar cuáles de las curvas graficadas (1, 2, 3) de energía en función del tiempo corresponden a las siguientes funciones a1) Energía disipada (calor) en la resistencia en función del tiempo a2) Energía almacenada en el capacitor en función del tiempo a3) Trabajo realizado por la batería en función del tiempo. b) Realizar un gráfico que represente la potencia instantánea de la batería en función del tiempo. c) En el mismo par de ejes del ítem (b) anterior realizar el gráfico de la potencia disipada instantánea en la resistencia en función del tiempo. 11 10 9 1 8 7 6 2 5 4 3 3 2 1 0 0 1 2 3 4 5 6 Tiempo (segundos) Las preguntas a), b y c) del problema 4) se deben justificar completamente con algunos de los siguientes recursos (pueden ser varios): desarrollos analíticos; valores del gráficos, datos del problema, propiedades de las funciones, propiedades del las curvas, conceptos físicos relevantes…etc. 5) Un capacitor está conectado a una batería de 9 Volt. Se lo desconecta de la batería y se coloca entre sus placas un voltímetro cuya resistencia interna es de 1,5 M. Al cabo de 1 minuto el voltímetro indica 2 Volt. a) ¿Cuánto vale la capacitancia del capacitor? Si se espera 1 minuto más, ¿cuál será la indicación del voltímetro? b) ¿Cuánta energía se disipó en la resistencia en esos 2 minutos? 2) Un capacitor de 2 mF, inicialmente descargado, se conecta a través de una resistencia R = 1 K con una batería 100 Volt. En el instante to = 0 se cierra la llave. a) Calcular la energía almacenada en el capacitor, la energía que se ha disipado en la resistencia en forma de calor y el trabajo realizado por la batería, entre to = 0 y t = 3 segundos. b) Realizar un gráfico que represente en un mismo par de ejes, la diferencia de potencial entre las placas del capacitor y la caída de potencial en la resistencia en función del tiempo entre to = 0 y t = 8 segundos. 3) Hallar el circuito equivalente de Thévenin entre A y B (Especificar el criterio por el cual se determinan sus elementos, desarrollar todos los cálculos y si es necesario mostrar las transformaciones del circuito) 4) Un capacitor de 2 mF, inicialmente descargado, se conecta a través de una resistencia R = 2 K con una batería 100 Volt. En el instante to = 0 se cierra la llave. a) Calcular la energía almacenada en el capacitor para t = 9 segundos. b) Calcular cuánta energía se ha disipado en la resistencia en forma de calor entre to = 0 y t = 9 segundos.