Problemas_Adicionales_1
Anuncio
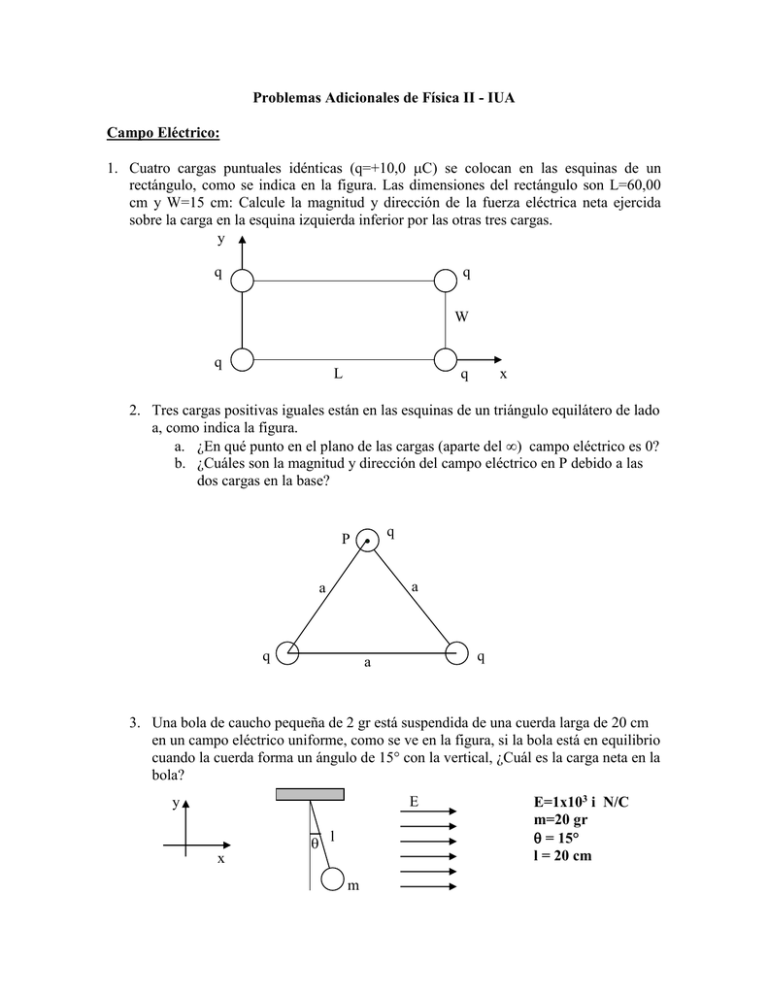
Problemas Adicionales de Física II - IUA Campo Eléctrico: 1. Cuatro cargas puntuales idénticas (q=+10,0 C) se colocan en las esquinas de un rectángulo, como se indica en la figura. Las dimensiones del rectángulo son L=60,00 cm y W=15 cm: Calcule la magnitud y dirección de la fuerza eléctrica neta ejercida sobre la carga en la esquina izquierda inferior por las otras tres cargas. y q q W q L q x 2. Tres cargas positivas iguales están en las esquinas de un triángulo equilátero de lado a, como indica la figura. a. ¿En qué punto en el plano de las cargas (aparte del ) campo eléctrico es 0? b. ¿Cuáles son la magnitud y dirección del campo eléctrico en P debido a las dos cargas en la base? q P a a q q a 3. Una bola de caucho pequeña de 2 gr está suspendida de una cuerda larga de 20 cm en un campo eléctrico uniforme, como se ve en la figura, si la bola está en equilibrio cuando la cuerda forma un ángulo de 15° con la vertical, ¿Cuál es la carga neta en la bola? E y l x m E=1x103 i N/C m=20 gr = 15° l = 20 cm 4. Dos esferas pequeñas cada una de 2 gr masa están suspendidas por medio de cuerdas ligeras de 10 cm de largo. Un campo eléctrico uniforme se aplica en la dirección de x. Si las esferas tienen cargas iguales a –q y +q, calcular el campo eléctrico E que permite a las esferas estar en equilibrio a un ángulo =10°. y l x m E Ley de Gauss: 5. Considere una caja triangular cerrada que descansa dentro de un campo eléctrico horizontal de magnitud E = 7,8 x 104 N/C, como indica la figura. Calcule el flujo eléctrico a través de a) la superficie vertical, b)la superficie inclinada, c)toda la superficie de la caja. 30 cm E 10 cm 6. Un cono de radio R en la base y la altura h esta sobre una mesa horizontal, y un campo eléctrico uniforme horizontal E penetra el cono, como muestra la figura. Determine el flujo eléctrico que penetra el cono. E h R 7. La línea ag de la figura es una diagonal del cubo, y una carga puntual q se localiza muy cerca del vértice a (en la extensión de ag), como se muestra en la figura. Determine el flujo eléctrico a través de cada lado del cubo que contiene al punto a. d q c b a h g e j Potencial Eléctrico: 8. Calcule la energía requerida para agrupar el arreglo de cargas que se muestran en la figura, donde a = 0,20 m, b = 0,40 m, y q = 6 C. q -2q a 2q 3q b 9. La figura muestra varias superficies equipotenciales cada una marcada por su potencial en volts. La distancia las distancias entre las líneas del cuadriculado representan 1 cm. A) La magnitud del campo es más grande en A o B ¿Por qué?. B) Represente como se observa el campo dibujando al menos ocho líneas de campo. A x 8 6 4 x 0 2 B Capacitancia y Dieléctricos: 10. Un capacitor de placas paralelas tiene un área de placas de 12 cm2 y una capacitancia de 7 pF. ¿Cuál es la separación entre placas?. 11. Un capacitor de aire variable que se usa en sintonización está echo de diez placas semicirculares, cada una de 2,5 cm de radio y separadas por 80 cm una de otra. Un segundo conjunto que gira libremente se intercala con el primer conjunto de placas. Determine la capacitancia como una función del ángulo de rotación , donde = 0 corresponde a la máxima capacitancia. R 12. Determine la capacitancia equivalente para la red de capacitores que se muestra en la figura. Si la red se conecta a una batería de 12 V, calcule la diferencia de potencial a través del capacitor y la carga en cada capacitor. 3 F 6 F 2 F 13. Considere el circuito mostrado en la figura, donde C1= 6 F, C2= 3 F y V = 20 V. El capacitor C1 se carga primero cerrando el interruptor S1. Este interruptor se abre después, y el capacitor cargado se conecta al capacitor descargado al cerrar S2. Calcule la carga inicial adquirida por el C1 y la carga final en cada capacitor. V C1 S1 C2 S2 Corriente Eléctrica y resistencia 14. Un conductor de 1,2 cm de radio conduce una corriente de 3 A producido por un campo eléctrico de 120 V/m. ¿Cuál es la resistividad del material?. 15. Una batería de 10 volt se conecta a un resistor de 120 , ignorando la resistencia interna de la batería. ¿Cuál es la potencia disipada por el resistor?. 16. Las baterías se especifican en términos de Amper. Horas, donde una batería de 1 A.h. a) ¿Cuál es la energía total, en KWH, almacenada en una batería de 12 Volt especificada con 55 A.h?. b)Cuál es el valor de la de la electricidad producida por esa bobina?. Circuitos Eléctricos: 17. Una batería tiene una fem de 15 volt. El voltaje terminal de la batería es de 11,6 V cuándo esta entrega 20 W de potencia a un resistor de carga externo R. a) ¿Cuál es el valor de R? B) ¿Cuál es la resistencia interna de la batería?. 18. La corriente en un circuito se triplica conectando un resistor de 500 en paralelo con la resistencia del circuito. Determine la resistencia del circuito en ausencia del resistor de 500 . 19. Tres resistores de 100 se conectan como se indica en la figura. La máxima potencia disipada en cualquiera de los resistores es de 25 W. a) ¿Cuál es el máximo voltaje que puede aplicarse a los terminales a y b. b) Para el voltaje obtenido en el inciso a ¿Cuál es la potencia disipada en cada resistor?. ¿Cuál es la potencia total disipada?. 100 a b 100 100 20. El circuito de la figura se ha conectado durante un largo tiempo. a) ¿Cuál es el voltaje a través del capacitor?. b) Si se desconecta la batería ¿cuánto tarda el capacitor en descargarse hasta 1/10 de su voltaje inicial?. RI = 1 RII = 4 RIII = 8 Rx = 2 C = 1 F. V = 10 V 21. Antes de que el interruptor se cierre en la figura, no hay carga almacenada en el capacitor. Determine las corrientes en las resistencias R1 y R2 y en C. A) en el instante en que el interruptor se cierra (es decir en t = 0), y b) después que el interruptor se cierra largo tiempo ( es decir t ∞ ). S R1 C R2 Datos: R1 = 10 K R2 = 5 K = 10 V C = 10 F 22. Tres focos eléctricos de 60 W y 120 Volt se conectan a través de la misma fuente de potencia como muestra la figura. Encuentre : a) la potencia total disipada en los tres focos, y b) en voltaje en cada uno. Suponga que la resistencia en cada foco concuerda con la Ley de Ohm (aun cuando en realidad la resistencia aumenta de manera notable con la corriente) 120 V R 1 R2 R3 Campos Magnéticos 23. Un conductor suspendido por dos alambres flexibles, como muestra la figura, tiene una masa por unidad de longitud de 0,040 Kg/m. ¿Qué corriente debe existir en el conductor para que la tensión en los alambres de soporte sea 0 cuando el campo magnético es de 3,6 T hacia el interior de la página?. ¿Cuál es la dirección requerida por la corriente.? x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x 24. Una barra de 0,72 Kg. de masa 6 cm de radio descansa sobre dos rieles paralelos, como muestra la figura, separados una distancia de 12 cm y una longitud l = 45 cm. La barra conduce una corriente de I= 48 A en la dirección indicada, y rueda a lo largo de los rieles sin fricción. Si la barra parte de reposo, ¿Cuál es la velocidad cuando deja los rieles si hay un campo magnético uniforme de 0,24 T en la dirección perpendicular a la barra de los rieles? d I B L 25. Un lazo rectangular consta de N = 100 vueltas enrolladas muy próximas entre sí y tiene dimensiones a = 0,40 m y b = 0,30 m. El lazo se articula a lo largo del eje y, y su plano forma un ángulo = 30° con el eje x, como indica la figura. ¿ Cuál es la magnitud del momento de torsión ejercido sobre el lazo por un campo magnético uniforme B = 0,80 T dirigido a lo largo del eje x cuando la corriente I = 1,2 A en la dirección indicada? ¿Cuál es la dirección esperada de rotación del lazo? Y I= 1,2 A 0,40 m 0,30 m Z X Ley de Faraday 26. Considere el arreglo mostrado en la figura. Suponga que R = 6 , l = 1,2 m y un campo magnético uniforme de 2,5 T apunta hacia adentro de la página. ¿A qué velocidad debe moverse la barra para producir una corriente de 0,5 A en el resistor? R l Fap 27. En la figura, el imán de la barra se mueve hacia el lazo ¿Va - Vb es positiva negativa o cero? (Explique) S N a R Movimiento hacia la curva b 28. Encuentre la potencia disipada en el resistor de 12 en la figura,: El campo magnético uniforme de 0,675 T está dirigido hacia adentro del plano del circuito y el conductor de 50 cm de largo se mueve a una velocidad v = 4,20 m/s x x x x x x x x x x x x x x x x x x x x x B x x x x x x x x x x x x v x x x x x x x x x 29. Una bobina cuadrada (20 cm X 20 cm) que consta de 100 vueltas de alambre gira alrededor de un eje vertical a 1500 rev/min, como se indica en la figura. La componente horizontal del campo magnético terrestre en la posición de la bobina es 2 x 10-5 T. Calcular la máxima f.e.m. inducida en la bobina por este campo. 20 cm 20 cm Inductancia 30. En el circuito que muestra la figura, el interruptor S1 se cierra primero y después de cierto tiempo la corriente que circula por L1 es 0,60 A. Luego se cierra el interruptor S2. Encuentre las corrientes a través de las bobinas en el momento en que el interruptor S2 se cierra. Suponga que las resistencias de las bobinas son despreciables y considere = 12 V, r = 10 , L1= 2 H y L2= 6 H. S1 S2 , r L1 L2 31. Considere el circuito de la figura. ¿Cuánta energía se almacena en el inductor cuando la corriente alcanza su valor de equilibrio final después de que se cierra el interruptor?. 8 12 V 4H S






