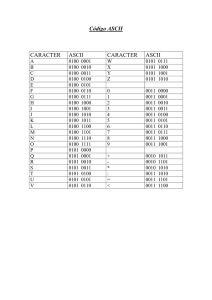
SISTEMA BINARIO ,OCTANO Y HEXDECIMAL
Anuncio

SISTEMA BINARIO ,OCTANO Y HEXDECIMAL Sistema decimal Es el de base 10 y es el que entiende de modo natural el ser humano. Es, por tanto, el sistema que se utilizará como referencia para conocer las cantidades representadas en los otros sistemas de numeración. Se suponen n cifras enteras y sin signo. Rango de representación: 0 <= X < 10^n Sistema binario Este es el sistema de numeración que utiliza el computador internamente. Este sistema de numeración es de base 2. Para convertir un número decimal a binario, se divide sucesivamente por 2, y se toman sucesivamente el último cociente y desde el último resto hasta el primero. Rango de representación: 0 <= X < 2^n Sistema octal Este es el sistema de numeración en base 8 y utiliza 8 símbolos para representar las cantidades. Dichos símbolos son: 0, 1, 2, 3, 4, 5, 6 y 7 y tienen el mismo significado que sus equivalentes decimales. La conversión de octal a binario se realiza mediante la siguiente tabla: Octal Binario 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 Rango de representación: 0 <= X < 8^n Sistema hexadecimal Este es el sistema de numeración en base 16 y utiliza 16 símbolos para representar las cantidades. Dichos símbolos son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E y F. Los diez primeros son los números decimales y tienen el mismo significado que en la numeración decimal. Los seis últimos son letras que representan: A=10, B=11, C=12, D=13, E=14 y F=15. La conversión de hexadecimal a binario se realiza mediante la siguiente tabla: Hexadecimal Binario 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 A 1010 B 1011 C 1100 D 1101 E 1110 F 1111 Rango de representación: 0 <= X < 16^n Sistema binario-decimal Los denominados códigos binario-decimales corresponden a una codificación por campos, en la que cada campo contiene el código de una cifra decimal. Como existen 10 posibles cifras decimales, del 0 al 9, cada campo deberá tener al menos 4 bits, por ser 24 = 16 > 10. DECIMAL BCD 8421 Aiken 2421 exceso de 3 Biquinario 5421 0 0000 0000 0011 0000 1 0001 0001 0100 0001 2 0010 0010 0101 0010 3 0011 0011 0110 0011 4 0100 0100 0111 0100 5 0101 1011 1000 1000 6 0110 1100 1001 1001 7 0111 1101 1010 1010 8 1000 1110 1011 1011 9 1001 1111 1100 1100