Dipolo paralelo al suelo
Anuncio
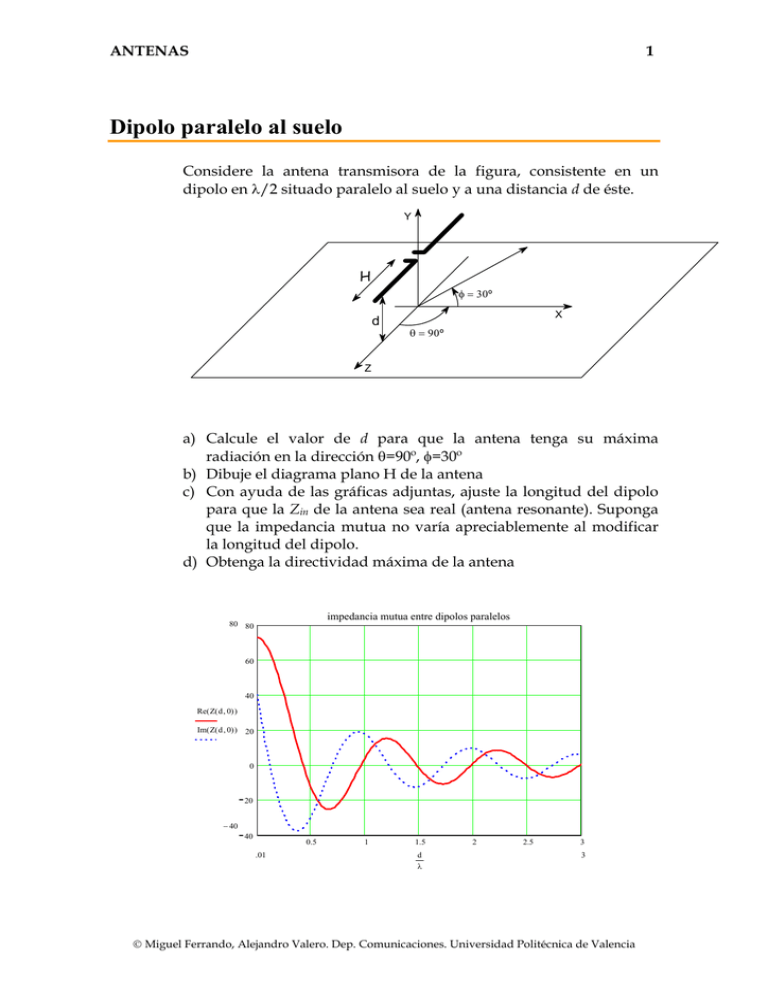
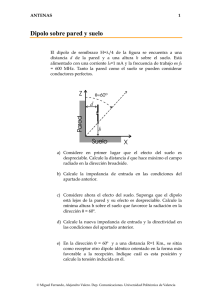
ANTENAS 1 Dipolo paralelo al suelo Considere la antena transmisora de la figura, consistente en un dipolo en λ/2 situado paralelo al suelo y a una distancia d de éste. Y H φ = 30º d X θ = 90º Z a) Calcule el valor de d para que la antena tenga su máxima radiación en la dirección θ=90º, φ=30º b) Dibuje el diagrama plano H de la antena c) Con ayuda de las gráficas adjuntas, ajuste la longitud del dipolo para que la Zin de la antena sea real (antena resonante). Suponga que la impedancia mutua no varía apreciablemente al modificar la longitud del dipolo. d) Obtenga la directividad máxima de la antena impedancia mutua entre dipolos paralelos 80 80 60 40 Re( Z( d , 0) ) Im( Z( d , 0) ) 20 0 20 − 40 40 0.5 .01 1 1.5 d λ 2 2.5 3 3 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 X11 para varios radios del dipolo 100 150 90 100 Im( Z1( H , .001 ) ) R11 para cualquier radio de dipolo 80 50 Im( Z1( H , .003 ) ) 70 Im( Z1( H , .005 ) ) Im( Z1( H , .007 ) ) Re( Z1( H , .001 ) ) 0 60 Im( Z1( H , .009 ) ) 50 50 100 150 40 0.2 0.22 0.24 30 0.26 0.2 0.22 0.24 H H Solución Campos radiados Aplicando la teoría de las imágenes, podemos sustituir el conjunto formado por el dipolo y el plano de masa por una pareja de dipolos con corrientes opuestas y separados una distancia 2d. G G G G El campo radiado por la antena es E = E0 e jkrˆ⋅r1 − e jkrˆ⋅r2 ( ) El diagrama de la antena es ⎛π ⎞ cos ⎜ cosθ ⎟ ⎝2 ⎠ ⋅ sen kd sen θ sen φ d (θ , φ ) = ( ) sen θ Si particularizamos en la dirección (θ, φ)=(90º,30º) resulta ⎛ kd ⎞ d (θ = 90º , φ = 30º ) = sen ⎜ ⎟ . ⎝ 2 ⎠ La expresión anterior se hace máxima cuando d=λ/2 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia 0.26 ANTENAS 3 Diagrama plano H El plano H, es el perpendicular al dipolo (plano θ=90º). Particularizando la expresión anterior d H (φ ) = sen (π sen φ ) Dado que en el plano H el diagrama del dipolo es omnidireccional, el diagrama de la antena es fruto de la interferencia del dipolo y su imagen. 90 120 0 60 0.8 0.6 150 30 0.4 0.2 F( φ ) 0 180 0 210 1 330 240 300 270 φ Impedancia de entrada c) La impedancia de entrada de un dipolo junto a un plano conductor es Z in = V1 = Z11 − Z12 (d = λ ) = ( R11 − R12 ) + j ( X 11 − X 12 ) I1 La separación entre los dipolos es 2d=λ. De la gráfica de impedancias mutuas obtenemos que Z12 ≅ 3 + j19 Ω Para que la antena sea resonante basta con elegir un dipolo tal que su reactancia sea también 19Ω. En las gráficas de la impedancia de entrada elegimos un semibrazo de H=0.241λ . © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 4 La resistencia de entrada que presenta la antena es Rin = 66 – 3 = 63 Ω Directividad La directividad máxima se calcula con Dmáx = Pmáx Wt / 4π r 2 El diagrama de este dipolo es como el de uno de longitud λ/2 a pesar de ser un poco más corto. Por lo tanto, incluyendo el factor de array debido a la imagen, Emáx = 120 I , Wt = Rin I 2 r Dmáx = 7.6 ( 8.8 dB) © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia