Dos dipolos ortogonales unidos por una línea de transmisión
Anuncio

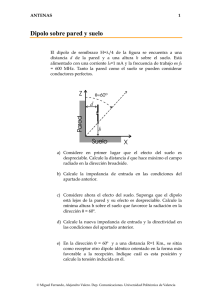
ANTENAS 1 Dos dipolos ortogonales unidos por una línea de transmisión Considere el montaje de la figura formado por un dipolo de semibrazo H1=5λ/8, orientado según el eje Z, y un dipolo de semibrazo H2=λ/4, orientado según el eje X, y unido al primero mediante una línea de transmisión de longitud l=λ/4 e impedancia característica Z0=87Ω. Suponga que los efectos mutuos son despreciables y por tanto la impedancia de entrada de los dipolos aislados es Z1=210-j600Ω y Z2=73Ω. a) Suponiendo que la frecuencia de trabajo es f=100 MHz, determine el valor de las bobinas que hay que añadir en la base del dipolo de semibrazo H1=5λ/8, para hacerlo resonante. b) Obtenga la relación entre las potencias radiadas y las corrientes máximas, Im1, Im2. c) Determine el valor del campo y la polarización en las direcciones de los ejes X, Y, Z. d) Suponga que en la dirección del eje Y se encuentra una espira ideal contenida en el plano YZ. Dibuje la variación de amplitud y fase de la tensión inducida en la espira cuando ésta se desplaza de la posición y = d (d<<λ) a la posición y= d+2λ z y x © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 Solución Adaptación del dipolo Para hacer resonante al dipolo de semibrazo H1=5λ/8,se debe compensar la parte reactiva de la impedancia. En este caso, dado el carácter capacitivo de la misma se añaden bobinas en la base. La impedancia que presenta el dipolo cargado en su base es Zin = 210 − j600 + 2(jωL) Ω La inductancia de cada una de las bobinas debe ser L= 600 H = 0.447 µ H 2 ⋅ 2π ⋅108 Análisis de la línea de transmisión b) Para obtener las corrientes a la entrada de los dipolos y posteriormente las corrientes máximas, planteamos el circuito equivalente de la antena I’2 I2 I1 Z0=87 Ω Z1 Z2 Z2 Z '2 = 0 Z2 l=λ/4 Tras transformar la impedancia Z2 en Z’2 podemos calcular la relación entre las corrientes I1 e I’2 Z1 I1 = Z '2 I '2 I1 103.7 = = 0.49 I '2 210 La relación entre la corriente I2 e I’2 se obtiene observando que la potencia radiada por el dipolo 2 es I '2 73 = I2 103.7 Despejando I’2 y sustituyendo en la anterior, se obtiene W2 = R '2 I '22 = R2 I 22 y por tanto © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 I1 = 0.414 I2 Podemos obtener la corriente máxima a partir de la corriente en bornes mediante I ( z ) = I m sen ⎡⎣ k ( H − z ) ⎤⎦ H1=5λ/8 : I1 (0) = I m1 Por tanto, H2=λ/4 : 1 2 I m1 = 0.586 Im2 I1 (0) = I m 2 Además de la relación de amplitudes calculada, debemos añadir una diferencia de fase de π/2 entre ambas corrientes debido al tramo de línea de λ/4. campos radiados El campo radiado por el dipolo de semibrazo H1=5λ/8 es G cos ( k z H1 ) − cos(kH1 ) N = zˆ 2kI m1 k 2 − k z2 G Nθ = N ⋅θˆ = − N z sen θ Eθ = − jω Aθ = j ωµ e − jkr N z sen θ 4π r © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 4 90 120 0.04 60 0.03 150 30 0.02 0.01 E( θ ) 180 0 0 210 330 240 300 270 θ El campo radiado por el dipolo de semibrazo H2=λ/4 es G cos ( k x H 2 ) − cos(kH 2 ) jk y λ4 ˆ N = x 2kI m 2 e k 2 − k x2 G ωµ e− jkr G ˆ G ˆ E=−j N ⋅θ + N ⋅ φ 4π r ( ) 90 120 60 0.02 150 30 0.01 E( θ ) 0 180 0 210 330 240 300 270 θ Así pues, los campos radiados totales en los ejes son: Eje x: el dipolo 2 tiene un nulo en esta dirección. El campo es el debido al dipolo 1. la polarización es lineal (vertical) Eje z: de manera análoga al caso anterior la radiación ahora se debe sólo al dipolo 2. La polarización es lineal Eje y: la radiación es la combinación de los campos de ambos dipolos. Se observa que los dipolos radian componentes ortogonales, de distinta amplitud y desfasados π/2, lo que se traduce en una polarización elíptica. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 5 Señal recibida por una espira La espira sólo capta la señal procedente del dipolo 1. el dipolo 2 y la espira tienen polarizaciones ortogonales y por lo tanto están desacopladas. Vca = − jωµ H x Sespira e − jkr ∝ r La amplitud de la tensión inducida es proporcional a La fase varía linealmente según − kr 1 r © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia