CO7 teoremas límite
Anuncio

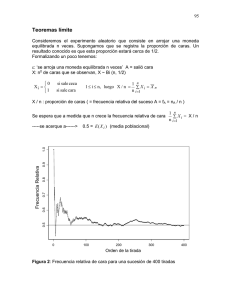
Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky 99 0.9 0.8 0.7 0.6 0.5 Frecuencia Relativa 1.0 12. Teoremas límite 0 100 200 300 400 Orden de la tirada Figura 1: Frecuencia relativa de cara para una sucesión de 400 tiradas. La figura 1 muestra las frecuencias relativas de cara obtenidas tomando tamaños crecientes desde 1 hasta 400, a partir de 400 tiradas sucesivas de una moneda. Las proporciones se acercan a 0.5 a medida que se obtienen utilizando una mayor cantidad de tiradas (los valores de Xi para las 20 primeras y 20 últimas tiradas fueron: (1 1 0 1 0 0 0 1 1 1 1 0 1 1 0 0 1 1 1 1) y (0 1 0 1 0 0 0 0 0 0 1 1 1 1 1 0 0 1 1 0) respectivamente) Es un resultado conocido que si se arroja una moneda muchas veces la proporción de caras (o de cecas) estará cerca de 1/2. La ley de los grandes números permite obtener ese resultado formalmente dentro de la teoría de probabilidades. 12.1 Ley (débil) de los Grandes Números Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky100 Sea X1, X2, ...., Xn, una sucesión de v.a. independientes tales que E(Xi) = μ y Var(Xi) = σ2 < ∞, entonces ∀ ε > 0 P( X n − μ > ε ) ⎯⎯ ⎯⎯→ 0 (1) n ⎯⎯→ ∞ n siendo X n = ∑X i =1 n i . E( X n ) = μ y Dem: Sabemos que Var ( X n ) = σ2 n , entonces aplicando la desigualdad de Chebishev a X n , P( X n − μ > ε ) ≤ y, por lo tanto ( Var ( X n ) ε2 σ2 = nε 2 ∀ε > 0 ) σ2 lim P X n − μ > ε ≤ lim 2 = 0 n →∞ n →∞ n ε ∀ε > 0 cqd. Cuando vale (1) decimos que la media muestral converge en probabilidad a μ, lo indicamos por p X n ⎯⎯→ μ U U También decimos que X n es un estimador consistente de μ Observación 1: La frecuencia relativa de un suceso A tiende a su probabilidad. U U Sea ε un experimento binomial que consta de n pruebas y sea Éxito= ocurrió el suceso A , P(A) constante en las n pruebas X: cantidad de veces que ocurrió A al realizar ε X ~ Bi (n, p), p =P(A) ⎧0 Xi = ⎨ ⎩1 no ocurre A ocurre A 1 ≤ i ≤ n, luego X / n = 1 n ∑ Xi = X n n i =1 X / n : = frecuencia relativa del suceso A = fA = nA / n p Por la LGN X n ⎯⎯→ μ , en este caso X n = X / n; E(Xi) = μ = p = P(A) luego p P(A) X / n n ⎯⎯→ Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky101 Observación 2 La desigualdad de Chebishev permite acotar la cantidad de repeticiones necesarias para que la frecuencia relativa del suceso A difiera de su probabilidad (P(A) = p ) en una cierta cantidad pre establecida (precisión), con una probabilidad alta determinada. U U Ejemplo: ¿Cuántas pruebas deberá tener el experimento ε para que la frecuencia relativa del suceso A difiera de su probabilidad (P(A) = p ) en como máximo 0.01 con probabilidad mayor o igual a 0.90? Queremos encontrar n tal que P( f A − p ≤ 0.01) ≥ 0.90 , (1) por Chebishev con ε = 0.01 tenemos que P( f A − p ≤ 0.01) ≥ 1 − p(1 − p) n (0.01) 2 (2) Luego la desigualdad (1) se cumplirá siempre que el último término de (2) sea mayor a 0.90: 1− p(1 − p) p(1 − p) p(1 − p) (3) ≥ 0.90 ⇔ ≤ 0.10 ⇔ n ≥ 2 2 (0.01) 2 (0.10) n (0.01) n (0.01) El valor mínimo de n depende de p a través de la expresión p(1-p) cuyo valor es máximo cuando p = 0.50. (Figura 2) Figura 2. Gráfico de la función f(p) = p*(1-p) para 0 ≤ p ≤ 1 Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky102 Por lo tanto, para alcanzar un mismo grado de precisión (en el ejemplo es 0.01) en la estimación de p el tamaño de la muestra depende del verdadero valor p (desconocido): p = 0.50 ⇒ n ≥ 25000 p = 0.10 ⇒ n ≥ 9250 p = 0.01 ⇒ n ≥ 990 Si se arroja la moneda 25000 veces se garantiza una precisión de 0.01 en la estimación de p para cualquier valor del mismo. Observación 3: Para que valga la ley de los grandes números es indispensable la existencia de la esperanza. U U Figura 3: comportamiento de la media muestral a medida que aumenta la cantidad de observaciones para una variable aleatoria N(8,1) y una variable aleatoria Cauchy centrada en 8 La figura 3 muestra que la sucesión correspondiente a la N(8,1) se acerca a su media (8) a medida que aumenta la cantidad de observaciones. La sucesión correspondiente a la distribución Cauchy muestra tendencias crecientes o decrecientes en algunos tramos, cambios abruptos en otros y no parece acercarse a su valor central (8). Esta distribución es un ejemplo para la cual no es válida la ley de los grandes números porque no está definida su esperanza. ¿Cómo es la distribución Cauchy? La función de densidad de probabilidad de una variable aleatoria Z llamada Cauchy centrada en cero es 1 f Z ( z) = −∞ < z < ∞ π (1 + z 2 ) y su función de distribución acumulada Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky103 1 1 + arctan( z ) − ∞ < z < ∞ 2 π ¿Qué forma tiene la función de densidad de la distribución Cauchy entrada en cero? FZ ( z ) = - Es simétrica con respecto al cero - Tiene forma de campana - Las colas tienden a cero más lentamente que la Normal Figura 4: funciones de densidad de probabilidad N(0,1) y Cauchy centrada en cero Debido a la simetría alrededor de cero de la función de densidad, la esperanza de una variable Cauchy debería ser cero. Sin embargo ∞ E(|Z|) = ∫ |z| −∞ π (1 + z 2 ) dz = 2∞ ∫ π z 0 (1 + z 2 ) dz = 2 π lim log(1 + a 2 ) = ∞ a →∞ La densidad de la variable Cauchy decrece a cero tan lentamente que valores grandes pueden ocurrir con una probabilidad relativamente alta impidiendo que la integral anterior converja. ¿ Cómo surge la distribución Cauchy? Se puede demostrar ( vea por ejemplo John Rice “Mathematical Statistics and Data Analysis” 1988-1995) que el cociente de dos variables aleatorias N(0,1) independientes tiene distribución Cauchy. 12.2 Corolario de la Ley de los Grandes Números Sea X1, ...,Xn una muestra aleatoria de una distribución con E(X i ) = μ Var(Xi ) = σ 2 < ∞ entonces y Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky104 p a) X ⎯⎯→ μ La media muestral converge en probabilidad a la media poblacional. Decimos que X es un estimador consistente de µ p b) S X2 ⎯ ⎯→ σ 2 La varianza muestral converge en probabilidad a la varianza poblacional. Decimos que S X2 estimador consistente de σ2 Dem. a) Ya lo vimos, por la Ley de los Grandes Números. b) Demostraremos que la varianza muestral S X2 es un estimador consistente de la varianza poblacional. n ⎞ ⎛ n 2 (X i − X )2 1 ⎛ n ⎟ ⎜ ∑ Xi ∑ n ⎜ i =1 2 2 2⎞ 2⎟ i =1 SX = −X = ⎜ ∑ X i − nX ⎟ = ⎟ n −1 n − 1 ⎝ i =1 ⎠ n −1⎜ n ⎟ ⎜ ⎠ ⎝ p Por la Ley de los Grandes Números X ⎯ ⎯→ μ , entonces p X2 ⎯ ⎯→ μ2. Por otra parte, aplicando nuevamente la Ley de los Grandes Números a X i2 n ∑X i =1 n Como además 2 i p ⎯ ⎯→ E ( X 2 ) = V ( X ) + [E ( X )] = σ 2 + μ 2 2 n → 1 , se obtiene n −1 ⎛ n 2 ⎞ ⎜∑ Xi ⎟ n ⎜ i =1 p 2 2⎟ −X ⎯ SX = ⎯→ σ 2 + μ2 − μ2 =σ 2 ⎜ ⎟ n −1 n ⎜ ⎟ ⎝ ⎠ y por lo tanto la varianza muestral es un estimador consistente de σ 2 . Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky105 12.3 Teorema Central del Límite: Sean X 1 , X 2 ,.... v.a. i.i.d con E ( X i ) = μ y Var( X i ) = σ 2 < ∞ , entonces si n es suficientemente grande, T − nμ ( a ) ~ N (0,1) nσ n ( X − μ ) (a) ~ N (0,1) σ con T = ∑ X i O sea ⎛ T − nμ ⎞ P⎜⎜ ≤ a ⎟⎟ ≅ Φ (a) ⎝ nσ ⎠ ⎛ n ( X − μ) ⎞ P⎜⎜ ≤ a ⎟⎟ ≅ Φ(a) σ ⎝ ⎠ donde Ф indica la función de distribución Normal estándar. Observaciones • Cualquiera sea la distribución de la variable de interés es posible aproximar la distribución de la suma de v.a.i.i.d por una distribución Normal, siempre que n sea suficientemente grande. • ¿Qué significa n suficientemente grande? ¿Cuándo es buena la aproximación? El tamaño de muestra requerido para que la aproximación sea razonablemente buena depende de la forma de la distribución de las Xi. Mientras más simétrica y acampanada sea, más rápidamente se obtiene una buena aproximación. 12.3.1 Aproximación de la distribución binomial por la normal Sea X la cantidad de éxitos en n repeticiones de un experimento de Binomial con probabilidad de éxito igual a p, entonces X ~ Bi (n,p) y sea X / n la proporción muestral de éxitos. Si definimos ⎧1 Xi = ⎨ ⎩0 si se obtuvo Éxito en la repetición i si se obtuvo Fracaso en la repetición i n para i = 1, ..., n. Entonces Xi ~ Bi (1, p) independientes y X = ∑ X i . i =1 Si n es suficientemente grande, del Teorema Central del Límite tenemos que Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky106 (a) X ~ N (np, np (1 − p ) ) X ( a ) ⎛ p (1 − p ) ⎞ ~ N ⎜ p, ⎟ n n ⎝ ⎠ Es decir que la distribución de, tanto la cantidad de éxitos como la proporción de éxitos en un experimento binomial, puede aproximarse por la distribución Normal. La aproximación es buena si n p ≥ 5 y n (1-p) ≥ 5. Si p = 0.5 la aproximación de la distribución binomial por la normal será buena aún para n pequeño pues en ese caso la distribución binomial es simétrica, como vemos en la figura siguiente. Figura 5: Distribuciones probabilidades de una v.a. X ~N(n,0.5) para distintos valores de n Recordemos que E(X) = np y Var(X)= np(1-p). A medida que n aumenta el valor central (np) se va corriendo a la derecha (figura 5), los “histogramas de probabilidad” se ensanchan y se achatan. Estadística (Q) FCEN-UBA Dra. Diana M. Kelmansky107 12.3.2 Corrección por continuidad Cuando se aproxima una distribución discreta por una continua, como es el caso de la aproximación de la distribución binomial por la normal, es necesario efectuar una corrección. Consideremos el siguiente ejemplo: Sea X ~ Bi (100, 0.5) y calculemos en forma aproximada P(X ≤ 51) y P(X ≥ 52). Recordemos que E(X) = 50 y Var(X) = 25 Si aplicamos directamente el TCL, obtenemos ( siendo Z ~ N(0,1)): ⎛ X − 50 51 − 50 ⎞ 1 ⎟⎟ ≅ P( Z ≤ ) = Φ(0.2) = 0.579 P( X ≤ 51) = P⎜⎜ ≤ 5 ⎠ 5 ⎝ 25 ⎛ X − 50 52 − 50 ⎞ 2 2 ⎟⎟ ≅ P( Z ≥ ) = P( Z ≤ − ) = Φ(−0.4) = 0.345 ≥ P( X ≥ 52) = P⎜⎜ 5 ⎠ 5 5 ⎝ 25 Utilizando la distribución binomial P(X ≤ 51) + P(X ≥ 52) = 1, pero dicho cálculo resultante de la aproximación Normal es 0.924. Se están subestimando las probabilidades. Es necesario realizar siguiente corrección, denominada corrección por continuidad: ⎛ X − 50 51.5 − 50 ⎞ P ( X ≤ 51) = P( X ≤ 51 + 0.5) = P⎜ ≤ ⎟ ≅ Φ(0.3) = 0.618 5 ⎝ 5 ⎠ ⎛ X − 50 51.5 − 50 ⎞ P ( X ≥ 52) = P( X ≥ 52 − 0.5) = P⎜ ≥ ⎟ ≅ Φ (−0.3) = 0.382 5 ⎝ 5 ⎠ En general, cuando la v.a. es discreta y xi – xi-1 = 1, la corrección se realiza en la forma: P( X ≤ a ) = P( X ≤ a + 0.5) P( X ≥ a ) = P( X ≥ a − 0.5) Observe que en las expresiones anteriores vale la igualdad. ¿Por qué? Si la distancia entre dos valores sucesivos de X es k > 1, ¿cómo aplicaría la corrección por continuidad? 12.3.3 Otras aplicaciones del Teorema Central del Límite Hemos visto ( sección 10.6 Sumas y más sumas) que si X 1 , X 2 ,...., X n son vaiid Estadística (Q) FCEN-UBA 1) Dra. Diana M. Kelmansky108 X i ~ Bi(ni , p) , entonces X i ~ Bi (1, p) ∀ i , entonces 2) X i ~ P (λi ) , i =1 i ⎛ n ⎞ ~ Bi⎜ ∑ ni , p ⎟. ⎝ i =1 ⎠ n ∑X i =1 entonces X i ~ ε (λ ) , entonces 4) X i ~ N (0,1) entonces 5) X i ~ ε (λ ) , entonces i ~ Bi(n, p). ⎛ n ⎞ ~ P⎜ ∑ λ i ⎟ . i =1 ⎝ i =1 ⎠ n ⎛ n ⎞ X i ~ Γ⎜ ∑ n i , λ ⎟ . ∑ i =1 ⎝ i =1 ⎠ n ∑X entonces X i ~ Γ ( ni , λ ) , 3) n ∑X i n ∑X i =1 i ~ Γ(n, λ ). n 2 ∑ X i ~ χ n = Γ( n / 2,1 / 2). i =1 n 2 ∑ X i ~ χ 22n i =1 En todas las sumas anteriores es posible, para n suficientemente grande, aproximar su distribución por una distribución Normal. Consideramos a continuación los casos particulares de distribuciones Poisson y Gamma: a) Sean X 1 , X 2 ,..., X n v.a. i.i.d. con distribución Poisson de parámetro λ, entonces n ∑X i =1 i ~ P(nλ ) Por lo tanto, cualquier v.a. con distribución de Poisson con parámetro suficientemente grande puede ser aproximada por la distribución normal. b) Sean X 1 , X 2 ,..., X n v.a. independientes con distribución Gamma de parámetros ni y λ, o sea X i ~ Γ(ni , λ ) entonces ⎛ n ⎞ X i ~ Γ⎜ ∑ n i , λ ⎟ ∑ i =1 ⎝ i =1 ⎠ n Por lo tanto, cualquier v.a. con distribución Γ(m, λ) con parámetro m suficientemente grande puede ser aproximada por la distribución normal.