C06 Variables Aleatorias

Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
87
10. Función de Probabilidad Conjunta
Dadas dos v.a. discretas, X e Y, definidas sobre el mismo espacio de probabilidad
de un experimento (Ω, P), la función de probabilidad conjunta para cada par de
números (x,y) es
pXY(x,y) = P(X = x, Y = y )
Observe que la probabilidad anterior corresponde a la probabilidad de una
intersección de sucesos. ¿Cuales sucesos?
Ejemplo 1:
Experimento aleatorio, ε: de una urna que contiene 4 bolitas rojas y 4 bolitas
blancas se extraen sucesivamente 3 bolitas sin reposición y se registra, en orden
de la extracción, el color de cada bolita extraida.
Espacio muestral, Ω = { bbb, rbb, brb, bbr, rrb, rbr, brr, rrr}
Variables aleatorias: X: Ω →R Y: Ω→ R definidas por
•
•
X = cantidad de bolitas rojas en las dos primeras extracciones
Y = cantidad de bolitas rojas en la 3ra. extracción.
La tabla siguiente muestra el espacio muestral del experimento Ω, una asignación
de probabilidades de cada suceso elemental y los valores que toman las variables
aleatorias X e Y en cada suceso elemental de Ω .
ϖ
bbb
rbb
brb
bbr
rrb
rbr
brr
rrr
P(ϖ)
(4/8)(3/7)(2/6)
(4/8)(4/7)(3/6)
(4/8)(4/7)(3/6)
(4/8)(3/7)(4/6)
(4/8)(3/7)(4/6)
(4/8)(4/7)(3/6)
(4/8)(4/7)(3/6)
(4/8)(3/7)(2/6)
X
0
1
1
0
2
1
1
2
Y
0
0
0
1
0
1
1
1
¿Es (Ω, P) un espacio de equiprobabilidad? ..................................................
P(X = 0, Y = 0) = P(bbb) = (4/8)(3/7)(2/6)= 1/14
Completamos la tabla de probabilidad conjunta de X e Y: pXY(x,y)
Estadística (Q)
FCEN-UBA
x
y
0
1
pX(x)
88
Dra. Diana M. Kelmansky
0
1
2
pY(y)
1/14
2/14
3/14
4/14
4/14
8/14
2/14
1/14
3/14
1/2
1/2
1
El par de v.a. (X , Y) se denomina vector aleatorio.
Las funciones pX y pY se llaman funciones de probabilidad marginales de X y de Y
respectivamente. Se obtienen a partir de la función de probabilidad conjunta por:
p X ( x) =
∑ p XY ( x, y )
pY ( y) =
y∈RY
∑ p XY ( x, y )
x ∈R X
10.1 Independencia de variables aleatorias
10.1.1 Independencia de dos variables aleatorias
Caso discreto. Diremos que X e Y son variables aleatorias independientes
(v.a.i.) si pXY(x,y) = pX(x) pY(y) para todo (x,y), es decir cuando
la función de probabilidad conjunta se factoriza
como el producto de las funciones de probabilidad marginales.
Siguiendo con el ejemplo 1: Como pXY(0,0) = 1/14 ≠ 3/4 *1/2
X e Y no son v.a.i
Caso continuo. Diremos que X e Y son v.a.i. si
fXY(x,y) = fX(x) fY(y) para todo (x,y) es decir cuando
la función de densidad conjunta se factoriza
como el producto de las funciones de densidad marginales.
10.1.2 Independencia de dos o más variables aleatorias
Diremos que una colección de n varibles aleatorias, X1, ..., Xn, definidas sobre el
mismo espacio de probabilidad de un experimento, son independientes si
∀ ( X 1 ,..., X k ) cumplen:
pX1,...,Xk (x1,...,xk ) = pX1 (x1)...pXk (xk )
en el caso discreto
Estadística (Q)
FCEN-UBA
89
Dra. Diana M. Kelmansky
f X1,...,Xk (x1,...,xk ) = f X1 (x1 ) .... f Xk (xk )
en el caso continuo
10.2 Funciones de variables y vectores aleatorios
Dado un vector aleatorio (X,Y) puede interesar determinar la distribución de una
variable aleatoria Z definida a partir de una función g(x,y):R2 → R. No
estudiaremos las condiciones generales para que esto sea posible.
Las funciones que veremos en este curso serán principalmente sumas, promedios
y productos.
10.2.1 Sumas de dos variables aleatorias
Sigamos con el espacio de probabilidad del ejemplo 1 y consideremos las
siguientes variables aleatorias:
X = cantidad de bolitas rojas en las dos primeras extracciones,
Y = cantidad de bolitas rojas en la 3ra. extracción
Z = cantidad de bolitas rojas en las 3 extracciones = X + Y
ϖ
bbb
rbb
brb
bbr
rrb
rbr
brr
rrr
x
0
1
1
0
2
1
1
2
P(ϖ)
(4/8)(3/7)(2/6)
(4/8)(4/7)(3/6)
(4/8)(4/7)(3/6)
(4/8)(3/7)(4/6)
(4/8)(3/7)(4/6)
(4/8)(4/7)(3/6)
(4/8)(4/7)(3/6)
(4/8)(3/7)(2/6)
y
0
0
0
1
0
1
1
1
x+y
0
1
1
1
2
2
2
3
La función de probabilidad puntual de Z , pZ, puede obtenerse tanto a partir de las
probabilidades definidas en el espacio muestral Ω como a partir de la tabla de
probabilidad conjunta de X e Y:
Por ejemplo
pZ(1) = (4/8)(4/7)(3/6) + (4/8)(4/7)(3/6) + (4/8)(3/7)(4/6) = 3(4/8)(3/7)(4/6) = 3/7
pZ(1) = pXY(0,1) + pXY(1,0) = 2/14 + 4/14 = 6 /14 = 3/7
Función de probabilidad puntual de Z
z
0
1
pZ(z)
1/14
6/14
2
6/14
3
1/14
1
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
90
10.3. Propiedades de la Esperanza y la Varianza
Hemos visto
a) Esperanza de una función de una variable aleatoria.
Sea X una v.a. con f.p.p. pX(x) y sea Y = h( X ) entonces E(Y) puede calcularse
como
 ∑ h( x i ) p X ( xi )
E(Y) =  i ≥ 1
 ∫ h (x) f X (x) dx
si X es discreta
si X es continua
Podemos generalizar
b) Esperanza de una función de dos variables aleatorias.
Sean X e Y v.a. con f.p.p. conjunta pXY(x,y) entonces E(g(X,Y)) puede calcularse
de la siguiente manera
 ∑ ∑ g( x , y ) p XY ( x , y )

E(g(X, Y) ) = 
 ∫ ∫ g( x , y ) f XY ( x , y ) d x d y

caso discreto
caso continuo
Consecuencias útiles
b)
c)
d)
e)
f)
g)
E(c) = c
E( aX + b) = aE(X) + b
Var (aX + b) = a2 Var(X)
E( X + Y ) = E( X ) + E( Y )
Var (X) = E ( X2 ) - E( X )]2
Var( X + Y ) = E [ (X+Y - E(X+Y) )2] = .............................
10.4 Covarianza
Sean X e Y dos v.a. con esperanzas µX y µY respectivamente, la covarianza
entre X e Y se define como
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
91

∑ (x − µ X )(y − µ Y )p XY (x, y)
 ∑
x y

Cov(X, Y) = E[(X − µ X )(Y − µ Y )] = 
∞ ∞
 ∫ ∫ (x − µ X )(y − µ Y )f XY (x, y)dx dy
− ∞ − ∞
según sean X e Y discretas o continuas.
Idea Intuitiva
Si X e Y son v.a. discretas y tienen una fuerte asociación positiva, serán más
probables los pares (x, y) en los que tanto x como y son grandes (mayores que
sus respectivas medias) (o ambos pequeños). Los productos ( x − µ X )( y − µ Y ) que
en esos casos son positivos contribuirán a la suma con probabilidades más altas.
Por lo tanto la suma de los ( x − µ X )( y − µ Y ) resultará positiva.
Por otra parte, si X e Y tienen una fuerte asociación negativa, en el sentido que
valores grandes de X aparecen con mayor probabilidad junto a valores
pequeños de Y y valores pequeños de X aparecen con valores grandes de Y,
entonces serán los productos ( x − µ X )( y − µ Y ) negativos (un factor será positivo y
el otro negativo, dando un producto negativo) los que tendrán mayores
probabilidades y por lo tanto la covarianza será negativa.
10.4.1 Propiedades de la covarianza
a) Cov(X, X) = Var(X) .
b) Cov(X, Y) = E(X Y) − E(X)E(Y).
c) Si X e Y son v.a. independientes, Cov (X,Y) = 0. La recíproca no es cierta en
general.
Ejemplo 2. Consideremos dos variables aleatorias con función de probabilidad
conjunta dada por la tabla siguiente
0
3
4
p X (x)
Y
X
0
1
2
3
4
1/5 0
0
0 1/5
0 1/5 0 1/5 0
0
0 1/5 0
0
1/5 1/5 1/5 1/5 1/5
pY ( y )
2/5
2/5
1/5
1
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
92
Vemos que
pXY (2, 3) = 0 ≠ pX (2) pY (3) = (1/5 ) (2/5)
Luego X e Y no son v.a. independientes y veamos que sin embargo Cov (X,Y) = 0
En efecto
1
1
1
E(XY) = 1 ⋅ 3 ⋅ + 2 ⋅ 4 ⋅ + 3 ⋅ 3 ⋅ = 4
5
5
5
1
1
1
1
1
E(X) = 0 ⋅ + 1 ⋅ + 2 ⋅ + 3 ⋅ + 4 ⋅ = 2
5
5
5
5
5
E(Y) = 0 ⋅
2
2
1
+ 3⋅ + 4⋅ = 2
5
5
5
Luego, Cov(X, Y) = 4 − 2 ⋅ 2 = 0.
Observación: La covarianza depende de las unidades.
10.4.2 Coeficiente de correlación
Sean X e Y dos v.a. con esperanzas µX y µY , desvíos estándar σ X > 0 y σ Y > 0 ,
respectivamente. El coeficiente de correlación entre X e Y se define como
ρ( X ,Y ) =
Cov( X , Y )
σ X σY
.
10.4.2.1 Propiedades del coeficiente de correlación
1) Sean a, b, c y d números reales y X e Y dos v.a. cualesquiera con varianza
positiva, entonces
ρ(aX + b, cY + d) = sg(ac) ρ(X, Y)
sg indica la función signo.
Observación: esta propiedad garantiza que el coeficiente de correlación no se
modifica al realizar un cambio en las unidades con que se expresan las variables.
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
93
2) − 1 ≤ ρ(X, Y) ≤ 1
3) ρ(X, Y) = 1 ⇔ Y = aX + b con probabilidad 1, para ciertos valores reales a y
b, a ≠ 0. Es decir: si el coeficiente de correlación es 1, en valor absoluto, los
pares (x,y) estarán sobre una recta
El coeficiente de correlación mide
el grado de asociación lineal entre las variables aleatorias.
10.5 Sumas y Promedios de Variables Aleatorias
Definición: Sea X1, ..., Xn una colección de n variables aleatorias, diremos que
esas variables constituyen una muestra aleatoria de tamaño n si
(a) las Xi’s son v.a. independientes
(b) todas las Xi’s tienen la misma distribución de probabilidades.
Cuando se cumplan (a) y (b) diremos en forma indistinta que:
las Xi’s son v.a. independientes e idénticamente distribuidas (v.a. i.i.d.)
Hemos visto que:
1) si los valores observados se obtienen mediante un muestreo aleatorio con
reposición de una población finita, (a) y (b) se cumplen exactamente
2) si el muestreo se realiza sin reposición de una población finita de tamaño N
mucho mayor que el tamaño muestral n, (a) y (b) se satisfacen
aproximadamente , pero a los fines prácticos pueden ser considerados
como una muestra aleatoria. Los valores observados de muestra aleatoria
(de las variables aleatorias X1, ..., Xn ) se los identifica por x1, ..., xn
x1, ..., xn ¡Son los DATOS!
Ya hemos visto en el capítulo de estadística descriptiva los siguientes estadísticos:
X=
1 n
∑ Xi
n i =1
n
Media Muestral,
T = ∑ Xi
i =1
Total Muestral
Son variables aleatorias. Les podemos calcular su esperanza y su varianza.
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
94
10.5.1 Esperanza y varianza de la suma de variables aleatorias
Veamos cual es la esperanza y la varianza de la suma de variables aleatorias i.i.d.
(la suma corresponde al total muestral si las v.a. son i.i.d)
n
n
i =1
i =1
n
n
i =1
i =1
E ( ∑ Xi ) = ∑ E ( Xi )
SIEMPRE!!!!
Var ( ∑ X i ) = ∑ Var ( X i )
SOLAMENTE cuando las v.a.
X1, ..., Xn son independientes
Ahora podremos demostrar fácilmente la siguiente proposición
10.5.2 Proposición
X~Bi ( n, p ) ⇒ E ( X ) = n p
y Var ( X ) = n p ( 1 - p )
Demostración: X = cantidad de éxitos en un experimento binomial.
n
X puede escribirse como una suma de v.a.i. X1, ..., Xn, o sea X = ∑ X i , donde
ii =1
Xi = cantidad de éxitos en la i -ésima prueba del experimento binomial - variable
Bernouilli
0 si el resultado es F
Xi = 
1 si el resultado es E
p X i (1) = p
p X i (0) = 1 - p
Para cada Xi tenemos que
E ( Xi ) = 0 pXi (0) + 1 pXi ( 1 ) = p
E ( Xi2) = 02 pXi (0) + 12 pXi ( 1 ) = p
Var ( Xi ) = E ( Xi2) - [E ( Xi )]2 = p - p2 = p (1 - p)
n
n
E ( X ) = E (∑ X i ) = ∑ E ( X i ) = np
Luego
ii =1
ii =1
n
Var ( X ) = Var (∑ X i )
ii =1
n
=
∑ Var ( X i ) = np(1 − p)
Independencia ii =1
como queríamos demostrar
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
95
10.5.3 Propiedades de la media muestral y la varianza muestral
Si X1, ..., Xn es una m.a. de una población con media µ y varianza σ2 entonces
i) E ( X ) = µ
X es un estimador insesgado de
µ
ii) Var ( X ) = σ 2 /n
iii) E ( S ) = E (
2
∑
n
(X i − X ) 2
i =1
n -1
) =σ
2
S2 es un estimador insesgado de
σ2
Dem iii)
Como E(Xi ) = µ Var(Xi ) =σ
Como
2
2
2
2
entonces E (Xi ) = µ +σ
E (X) = µ Var(X) = σ 2/n entonces E (X) = µ2 +σ 2/n
Además
E(
∑
n
i =1
∑
(X i − X ) 2 ) =
n
i =1
E (X i2 − 2X i X + X 2 ) = ∑i =1 ( E (X i2 ) − 2 E (X i X ) + E ( X 2 ))
n
Consideremos las esperanzas anteriores
1) E (X i2 ) = σ 2 + µ 2
∑X
2) como X i X =
∑µ
E(X i X ) =
i≠ j
n
i≠ j
i
Xj
n
X2
+ i resulta E(X i X ) =
n
∑ E( X
i≠ j
n
i
X j)
+
E ( X i2 )
por lo tanto
n
2
+
σ 2 + µ2
n
2
2
3) E (X) = µ +σ /n
Finalmente de 1), 2) y 3) tenemos que
n
n
∑i =1 ( E (X i2 ) − 2E (X i X ) + E ( X 2 )) = ∑i =1 (σ 2 + µ 2 − 2(σ 2 + µ 2 / n) + σ 2 / n + µ 2 ) = σ 2 (n − 1)
cqd
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
96
10.6 Sumas y más sumas
En general es difícil calcular la distribución de la suma o de una combinación lineal de n
v.a. independientes, aún cuando tengan la misma distribución. Sin embargo, en los casos
siguientes, la distribución de la suma o de combinaciones lineales es conocida.
Sean X 1 , X 2 ,...., X n v.a. independientes. Si
n
1)
X i ~ Bi(ni , p ) ,
entonces
X i ~ Bi (1, p) ∀ i ,
entonces
i =1
∑X
i
i =1
entonces
∑X
i
i =1
~ Bi (n, p).
 n 
~ P ∑ λi  .
 i =1 
 n

~ Γ ∑ n i , λ  .
 i =1

n
entonces
X i ~ ε (λ ) ,
entonces
5)
X i ~ (0,1)
entonces
6)
X i ~ ε (λ ) ,
entonces
7)
 n

~ Bi ∑ ni , p .
 i =1

n
X i ~ Γ ( ni , λ ) ,
4)
i
n
2) X i ~ P (λi ) ,
3)
∑X
∑X
i =1
i
n
∑X
i =1
n
i
~ Γ(n, λ ).
∑ X i ~ χ n = Γ(n / 2,1 / 2).
2
i =1
n
X i ~ ( µ i , σ i2 )
y
2 ∑ X i ~ χ 22n
i =1
a1 , a 2 ,..., a n
son
números
reales,
n
n
n

Y = ∑ a i X i ~  ∑ a i µ i , ∑ a i2σ i2  .
i =1
i =1
 i =1

En particular, si X i ~ ( µ , σ 2 ) , entonces
i)
iii)
n
T = ∑ X i ~ ( nµ , nσ 2 )
i =1
n
(X − µ)
σ
~ (0 ,1)
ii)
 σ2
X ~  µ ,
n





.
entonces
Estadística (Q)
FCEN-UBA
Dra. Diana M. Kelmansky
97
11 Desigualdad de Chebishev
Para calcular la probabilidad de un suceso en términos de una v.a. X es necesario
conocer la distribución de la v.a. La desigualdad de Chebishev provee una cota
que no depende de la distribución sino sólo de la varianza de X, para el cálculo de
la probabilidad de un tipo de sucesos. Una de sus formas provee además una
interpretación de la varianza.
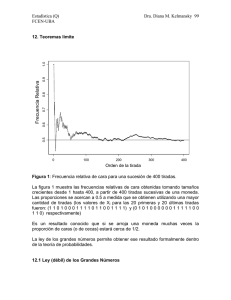
Figura 1
Proposición: Sea X una v.a. con media µ y varianza σ2 < ∞, entonces
P( X − µ > ε ) ≤
∀ ε > 0,
σ2
ε2
Dem: Lo haremos para el caso continuo. La demostración para el caso discreto es
similar.
∞
σ 2 = E (( X − µ ) 2 ) = ∫ ( x − µ ) 2 f ( x) dx =
−∞
=
≥
2
∫ ( x − µ ) f ( x) dx +
{ x / x − µ >ε }
∫ (x − µ)
{ x / x − µ >ε }
2
∫ ( x − µ ) f ( x) dx ≥
{ x / x − µ ≤ε }
2
f ( x ) dx
∫ ε f ( x) dx = ε P( X − µ
{ x / x − µ >ε }
≥
2
Entonces,
σ2
≥ P( X − µ > ε )
ε2
Como queríamos demostrar.
Observemos
2
> ε)
Estadística (Q)
FCEN-UBA
•
•
•
Dra. Diana M. Kelmansky
98
No se pide nada sobre la distribución de X, salvo que la varianza tiene que ser
finita.
la desigualdad nos muestra que cuanto más pequeño sea σ2 tanto más
pequeña será la probabilidad de que X esté lejos de µ.
La cota que provee la desigualdad de Chebishev puede ser grosera o, peor
aún, no informativa, por ejemplo, si ε ≤ σ2.
Otras formas de la desigualdad de Chebishev: Otras formas equivalentes de la
desigualdad de Chebishev son las siguientes.
a)
∀ ε > 0,
b)
∀ k ≥ 1,
P( X − µ ≤ ε ) ≥ 1 −
P( X − µ > kσ ) ≤
σ2
ε2
1
k2
En la desigualdad planteada en b) se destaca cómo el desvío estándar mide el
grado de “concentración” de la distribución alrededor de la media µ = E(X). De
aquí resulta que para cualquier conjunto de datos la proporción de ellos que está a
una distancia del promedio mayor que k veces σ es a lo sumo 1 / k2
k
2
3
4
5
6
7
8
1/k2
0.2500
0.1111
0.0625
0.0400
0.0278
0.0204
0.0156
Si X tiene distribución Normal ( X ~ N(µ, σ2) ) podemos calcular exactamente la
probabilidad que X difiera de su media, en valor absoluto, más de 2 veces su
desvío estándar, es decir
P ( | X - µ | > 2 σ ) = 0.045
Esta probabilidad es acotada por 0.25 mediante la desigualdad de Chebishev