FACULTAD DE CC. ECONÓMICAS Y EMPRESARIALES GRADO
Anuncio

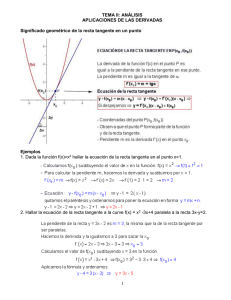
FACULTAD DE CC. ECONÓMICAS Y EMPRESARIALES GRADO EN ADE MATEMÁTICAS EMPRESARIALES I 22 – JUNIO -2010 Apellidos y nombre:_____________________________________________________________DNI______________ TEST: Cada pregunta bien contestada suma 5 puntos. Cada una mal contestada resta 2 puntos 1. La función f ( x) x 3 3x 2 p toma el valor 2 en algún punto del intervalo [1, 2]: a) Cualquiera que sea el valor de p. b) Si p = 5 c) Ninguna de las anteriores 2 2. La función f ( x) x 4 es discontinua en x 2 3x 2 x = -2. Tal discontinuidad puede evitarse definiendo: a) f(-2) = 1/4 b) f(-2) = 0 c) Ninguna de las anteriores 2 3.- La función g ( x) ax( x 2) si x 2 es 2 ax 3 si x 2 derivable en todo R si: a) a = 4 b) a = 1/4 c) Nunca. x 4.- La función f ( x) 2 2x e , en el intervalo (0, 1), cumple: a) Corta una vez al eje OX. b) Tiene un máximo. c) Ninguna de las anteriores. 5.- La recta tangente de la función f ( x) x 2 4a 1en el punto x=0 es: a) y 1 4ax b) y 1 4ax c) Ninguna de las anteriores, sino la recta__________________ 6.- La función f ( x) x 3 tiene en x=0: a) Un máximo b) Un mínimo c) Un punto de inflexión 7.- El área que encierra la gráfica f ( x) x 2 entre los puntos x=-1 y x=1 es: a) 1/3 b) 2/3 c) Ninguna de las anteriores: la respuesta es:___________________ 8.- La función derivada de f ( x ) Ln x x es: a) b) c) 1 x Ln x 1 f ' ( x) x2 1 Ln x f '( x) x2 f ' ( x) 9.- El límite de f ( x) x2 x cos x cuando x 0 es: a) 0 b) 1/2 c) -2 10.- La ecuación de la recta tangente a la curva f ( x) 2 x 3 6 x 2 4 en su punto de inflexión es: a) y = –6x –1 b) y = –x – 6 c) y = –6x – 6 FACULTAD DE CC. ECONÓMICAS Y EMPRESARIALES GRADO EN ADE MATEMÁTICAS EMPRESARIALES I 22 – JUNIO -2010 Apellidos y nombre:_____________________________________________________________DNI______________ TEST: Cada pregunta bien contestada suma 5 puntos. Cada una mal contestada resta 2 puntos b) y 1 4ax c) Ninguna de las anteriores, sino la recta__________________ 1. La función f ( x) x 3 3x 2 p toma el valor 2 en algún punto del intervalo [1, 2]: a) Cualquiera que sea el valor de p. b) Si p = 5 c) Ninguna de las anteriores 2. La función f ( x) x 3 tiene en x=0: a) Un máximo b) Un mínimo c) Un punto de inflexión 2 3.- La función f ( x) x 4 es discontinua en x 2 3x 2 x = -2. Tal discontinuidad puede evitarse definiendo: a) f(-2) = 1/4 b) f(-2) = 0 c) Ninguna de las anteriores 2 4.- La función g ( x) ax( x 2) si x 2 es 2 ax 3 si x 2 derivable en todo R si: a) a = 4 b) a = 1/4 c) Nunca. x 5.- La función f ( x) 2 2x e , en el intervalo (0, 1), cumple: a) Corta una vez al eje OX. b) Tiene un máximo. c) Ninguna de las anteriores. 6.- La recta tangente de la función f ( x) x 2 4a 1en el punto x=0 es: a) y 1 4ax 7.- El límite de f ( x) x2 x cos x cuando x 0 es: a) 0 b) 1/2 c) -2 8.- La ecuación de la recta tangente a la curva f ( x) 2 x 3 6 x 2 4 en su punto de inflexión es: a) y = –6x –1 b) y = –x – 6 c) y = –6x – 6 9.- El área que encierra la gráfica f ( x) x 2 entre los puntos x=-1 y x=1 es: a) 1/3 b) 2/3 c) Ninguna de las anteriores: la respuesta es:___________________ 10.- La función derivada de f ( x ) Ln x x es: a) b) c) f ' ( x) 1 x f ' ( x) Ln x 1 x2 f '( x) 1 Ln x x2 FACULTAD DE CC. ECONÓMICAS Y EMPRESARIALES GRADO EN ADE MATEMÁTICAS EMPRESARIALES I 22 – JUNIO -2010 Apellidos y nombre:_____________________________________________________________DNI______________ TEST: Cada pregunta bien contestada suma 5 puntos. Cada una mal contestada resta 2 puntos 1. La función f ( x) x 3 3x 2 p toma el valor 2 en algún punto del intervalo [1, 2]: a) Cualquiera que sea el valor de p. b) Si p = 5 c) Ninguna de las anteriores 2. El área que encierra la gráfica f ( x) x 2 entre los puntos x=-1 y x=1 es: a) b) c) 1/3 2/3 Ninguna de las anteriores: la respuesta es:___________________ 3.- La función derivada de f ( x ) Ln x x es: a) b) c) 1 f ' ( x) x Ln x 1 f ' ( x) x2 1 Ln x f '( x) x2 6.- La función f ( x) x 3 tiene en x=0: a) b) c) Un máximo Un mínimo Un punto de inflexión x 2 4 es discontinua en x 2 3x 2 x = -2. Tal discontinuidad puede evitarse definiendo: 7.- La función f ( x) a) b) c) f(-2) = 1/4 f(-2) = 0 Ninguna de las anteriores 2 8.- La función g ( x) ax( x 2) si x 2 es 2 ax 3 derivable en todo R si: a) b) c) a=4 a = 1/4 Nunca. 4.- La recta tangente de la función f ( x) x 2 4a 1en el punto x=0 es: a) b) c) y 1 4ax y 1 4ax Ninguna de las anteriores, sino la recta__________________ x 5.- .- La función f ( x) 2 2x e , en el intervalo (0, 1), cumple: a) b) c) Corta una vez al eje OX. Tiene un máximo. Ninguna de las anteriores. si x 2 9.- El límite de f ( x) a) b) c) x2 x cos x cuando x 0 es: 0 1/2 -2 10.- La ecuación de la recta tangente a la curva f ( x) 2 x 3 6 x 2 4 en su punto de inflexión es: a) b) c) y = –6x –1 y = –x – 6 y = –6x – 6 FACULTAD DE CC. ECONÓMICAS Y EMPRESARIALES GRADO EN ADE MATEMÁTICAS EMPRESARIALES I 22 – JUNIO -2010 Apellidos y nombre:_____________________________________________________________DNI______________ TEST: Cada pregunta bien contestada suma 5 puntos. Cada una mal contestada resta 2 puntos 1.La función derivada de f ( x ) Ln x es: x a) b) c) 1 x Ln x 1 f ' ( x) x2 1 Ln x f '( x) x2 f ' ( x) a) b) c) 6.- La recta tangente de la función f ( x) x 2 4a 1en el punto x=0 es: a) b) c) 2.- La función f ( x) x 3x p toma el valor 3 2 2 en algún punto del intervalo [1, 2]: a) Cualquiera que sea el valor de p. b) Si p = 5 c) Ninguna de las anteriores 3.- El área que encierra la gráfica f ( x) x 2 entre los puntos x=-1 y x=1 es: a) b) c) 1/3 2/3 Ninguna de las anteriores: la respuesta es:___________________ x 4 es discontinua en x 2 3x 2 x = -2. Tal discontinuidad puede evitarse definiendo: 4.- La función f ( x) a) b) c) 2 f(-2) = 1/4 f(-2) = 0 Ninguna de las anteriores 2 5.- La función g ( x) ax( x 2) si x 2 es 2 ax 3 derivable en todo R si: a=4 a = 1/4 Nunca. si x 2 y 1 4ax y 1 4ax Ninguna de las anteriores, sino la recta__________________ x 7.- La función f ( x) 2 2x e , en el intervalo (0, 1), cumple: a) Corta una vez al eje OX. b) Tiene un máximo. c) Ninguna de las anteriores. 8.- La función f ( x) x 3 tiene en x=0: a) b) c) Un máximo Un mínimo Un punto de inflexión 9.- El límite de f ( x) a) b) c) x2 x cos x cuando x 0 es: 0 1/2 -2 10.- La ecuación de la recta tangente a la curva f ( x) 2 x 3 6 x 2 4 en su punto de inflexión es: a) b) c) y = –6x –1 y = –x – 6 y = –6x – 6 PROBLEMAS 2 1 (20 puntos). Dibujar la gráfica de la función f ( x) ( x 1) , determinando sus intervalos de crecimiento, x 1 máximos, mínimos y asíntotas. 2 (10 puntos) Sea f ( x) ax3 bx2 cx d un polinomio que cumple f(1) = 0, f ´(0) = 2, y tiene dos extremos relativos para x = 1 y x = 2. a) Determinar a, b, c y d. b) ¿Son máximos o mínimos los extremos relativos? 3 (10 Puntos) Calcula las siguientes integrales: 4. (10 puntos) Hallar el polinomio de Taylor de grado 4, en el origen, de la función polinomio para calcular cos 0,1. . Utilizar dicho 1. La función f ( x) x 3 3x 2 p toma el valor 2 en algún punto del intervalo [1, 2]: a) Cualquiera que sea el valor de p. b) Si p = 5 c) Ninguna de las anteriores Solución: Esta función es continua siempre; en particular en el intervalo [1, 2]; además: f (1) 2 p y f (2) 4 p Por el teorema de los valores intermedios, la función toma todos los valores comprendidos entre 2 + p y 4 + p. Para que 4 p 2 2 p debe cumplirse que 2 2 p 4 2 . El valor p = 5 está entre esos valores. 2. La función f ( x) x2 4 es discontinua en x = 2. Tal discontinuidad puede evitarse x 2 3x 2 definiendo: a) f(2) = 1/4 b) f(2) = 0 c) Ninguna de las anteriores..(vale 4) Solución: En x = 2 la discontinuidad es evitable, pues existe el límite: x2 4 x2 0 lím 4 x 2 x 2 3x 2 x 2 x 1 0 lím ax ( x 2 2) si x 2 3. La función g ( x) es derivable en todo R si: 2 si x 2 ax 3 a) a = 4 b) a = 1/4 c) Nunca Solución: No puede ser derivable en x=2 porque no es continua en dicho punto, pues: si x 2–, g(x) 4a; si x 0+, g(x) 4a-3, por tanto nunca coinciden sea cual sea el valor de a, y al no ser continua no puede ser derivable en 2. x 4 - La función f ( x) 2 2x e , en el intervalo (0, 1), cumple: a) Corta una vez al eje OX. b) Tiene un máximo. c) Ninguna de las anteriores. x x x Sol. f ( x) 2 2x e f ´(x) 2 e f ´´(x) e La derivada primera se anula si x = ln 2 (0, 1). Como f ´´(ln 2) < 0, la función tendrá un máximo en x = ln 2. 5.- La recta tangente de la función f ( x) x 2 4a 1en el punto x=0 es: a) y 1 4ax b) y 1 4ax c) Ninguna de las anteriores, sino la recta_____ y = –4a+1_______ Solución: f ´(x)= 2x f ´(0)= 0, entonces la recta tangente en ese punto es y+4a-1 = 0(x – 0) y = –4a+1 6.- La función f ( x) x 3 tiene en x=0: a) Un máximo b) Un mínimo c) Un punto de inflexión Solución: Es un punto de inflexión, pues se anulan las dos primeras derivadas en ese punto. 7.- El área que encierra la gráfica f ( x) x 2 entre los puntos x=-1 y x=1 es: a) 1/3 b) 2/3 c) Ninguna de las anteriores: la respuesta es:___________________ Solución: 1 x3 2 2 A = x dx 1 3 3 3 1 1 2 8.- La función derivada de f ( x ) b) 1 x Ln x 1 f ' ( x) x2 c) f '( x) a) Ln x x es: f ' ( x) 1 Ln x x2 Solución: f '( x) c) es la solución, 1 Ln x x2 x2 0 es: 9.- El límite de f ( x) x cos x cuando x a) 0 b) 1/2 c) -2 Solución El límite vale 0. 10.- La función f ( x) 2 x 3 6 x 2 4 f´(x)=6x2-12x = 0 si x=0 o x=2f´´(x)=12x-12 f´´(0)=-12en x=0 hay un máximo: (0, 4). f´´(2)=-4en x=2 hay un mínimo: (2, -4). PROBLEMAS 1. Dibujar la gráfica de la función f ( x) ( x 1) 2 , determinando sus intervalos de x 1 crecimiento, máximos, mínimos y asíntotas. Solución: f ( x) ( x 1) 2 4 x 3 x 1 x 1 Luego: ASÍNTOTAS: x = –1 es una asíntota vertical.porque lím x 1 f ( x) x No tiene asíntotas horizontales porque lím f ( x) x y = mx+n=x – 3 es una asíntota oblicua. m = lím x f ( x) 1 y x n = lím( f ( x) mx) 3 , por tanto, la A.O es y = x-3. x (5 puntos) CRECIMIENTO , MÁXIMOS Y MÍNIMOS Derivada: f ´(x) ( x 1)(x 3) ( x 1) 2 f ´(x) = 0 en x = –3 y en x = 1 Si x < –3, f ´(x) > 0 f (x) crece. Si –3 < x < –1, f ´(x) < 0 f (x) decrece. Si –1 < x < 1, f ´(x) < 0 f (x) decrece. Si x > 1, f ´(x) > 0 f (x) crece. Es obvio que en x = –3 hay un máximo y en x = 1 un mínimo. Puntos (–3, –8) y (1, 0). (10 puntos) La gráfica aproximada de la función es la dada a continuación. (5 puntos) 2 Sea f ( x) ax3 bx2 cx d un polinomio que cumple f(1) = 0, f ´(0) = 2, y tiene dos extremos relativos para x = 1 y x = 2. a) Determinar a, b, c y d. b)¿Son máximos o mínimos los extremos relativos? Solución: a) (1) f(1)= a+b+c+d= 0 (2) f´(0) = c = 2 (3) f´(1) = 3a+2b+c=0 (4) f´(2) = 12a+4b+c=0 Tenemos 4 ecuaciones y cuatro incógnitas que resolviendo dan el resultado: a=1/3, b=-3/2, c=2, d=-5/6 b) f´´(x)= 2x-3; f´´(1)=-1<0, en x=1 hay un Máximo f´´(2)=1 >0; en x=2 hay un Mínimo 3). Calcula las siguientes integrales (1 punto): a) cos 4 xsenxdx cos5 C 5 b) e x sene x dx cos e x C Problema 4 (1 punto) Hallar el polinomio de Taylor de grado 4, en el origen, de la función f ( x) cos x . Utilizar dicho polinomio para calcular cos 0,1. Solución: a) f(x) = cos x; f´(x) = –sen x; f´´(x) = –cos x; f´´´(x) = sen x; f(4(x) = cos x; en x=0 tenemos que f(0) = cos 0=1; f´(0) = –sen x=0; f´´(=) = –cos x=-1; f´´´(0) = sen x=0; f(4(x) = cos x=1; P( x) 1 x2 x4 2 4! b) P(0,1) 1 0,12 0,14 0,9950041667; 2 4!