TEMA II: ANÁLISIS APLICACIONES DE LAS DERIVADAS

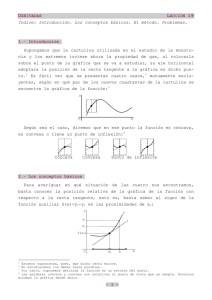
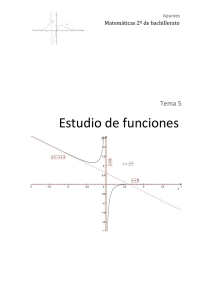
TEMA II: ANÁLISIS
APLICACIONES DE LAS DERIVADAS
Significado geométrico de la recta tangente en un punto
Ejemplos
1. Dada la función f(x)=x2 hallar la ecuación de la recta tangente en el punto x=1.
2. Hallar la ecuación de la recta tangente a la curve f(x) = x2 -3x+4 paralela a la recta 3x-y=2.
1
Análisis de una función:
Monotonía (Crecimiento y Decrecimiento)
Asíntotas
2
Extremos Relativos (Máximos y Mínimos)
Concavidad y Convexidad
Concavidad: Una función f(x) es cóncava en un
intervalo si el segmento de recta que une dos
puntos cualesquiera de su gráfica queda por
debajo de la gráfica o cuando las tangentes a la
curva en los puntos de dicho intervalo quedan
por encima de la curva.
3
Convexidad: Una función f(x) es convexa en
un intervalo si el segmento de recta que une
dos puntos cualesquiera de su gráfica queda
por encima de la gráfica o cuando las
tangentes a la curva en los puntos de dicho
intervalo quedan por encima de la curva.
Punto de Inflexión: Si f’(x0) = 0 y f(x)
cambia su curvatura (de cóncava a convexa
o al contrario) en el punto x0 entonces la
función f(x) tiene un punto de inflexión en x0.
EJEMPLO
Monotonía y Extremos:
4
Curvatura y Puntos de Inflexión:
Asíntotas:
Vertical:
Oblicua: No existe Asíntota Oblicua.
5
EJERCICIOS PROPUESTOS
1. Estudia los intervalos de crecimiento de las siguientes funciones:
a) f(x)=x3-3x2-9x+1
b) f(x) = x3/ (x2-4)
c) f(x) = ex (x2-3x+1)
2. Analiza por qué la gráfica de la función f(x)=3x-sen x no puede tener extremos relativos.
3. Halla los máximos y mínimos de las siguientes funciones:
a) f(x)=sen x + cos x en el intervalo [0;2π]
b) f(x) = x ln x
c) f(x) = x/ ex
4. Halla los puntos de inflexión de la función f(x)=ln(x2+1) y estudia su curvatura.
5. Dada f(x)=1-(2-x)5 , comprueba que f’(2)=0, f’’(2)=0 y f’’’(2)=0. ¿Tiene la función f máximo,
mínimo o punto de inflexión en x=2?
6. Halla los coeficientes a, b, c, d de la función f(x)=ax3+bx2+cx+d sabiendo que la ecuación de
la tangente a la curva en el punto de inflexión (1;0) es y=-3x+3, y que la función f tiene un
extremo relativo en x=0.
7. El propietario de un inmueble tiene alquilados cuarenta pisos a 300 euros al mes cada uno.
Por cada 10 euros de aumento en el precio del alquiler pierde un inquilino, que se traslada a
otro piso más económico. ¿Cuál es el precio del alquiler que más beneficios proporciona al
propietario?
8. En un jardín con forma de semicírculo de radio 10 m se va a instalar un parterre rectangular,
uno de cuyos lados está sobre el diámetro y el opuesto a él tiene sus extremos en la parte
curva. Calcula las dimensiones del parterre para que su área sea máxima.
9. Un nadador, A, se encuentra a 3 km de la playa enfrente de una caseta. Desea ir a B, en la
misma playa, a 6 km de la caseta. Sabiendo que nada a 3 km/h y anda por la arena a 5 km/h,
averigua a qué lugar debe dirigirse a nadao para llegar a B en el menor tiempo posible.
10. Estudia las funciones polinómicas y racionales que aparecen a continuación. Calcula en cada
una de ellas: Dominio, Asíntotas, Puntos de cortes con los ejes, Crecimiento y decrecimiento,
Máximos y mínimos y Puntos de inflexión.
6