Tabla de termodinámica
Anuncio

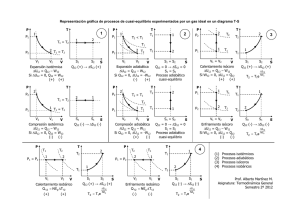
Ecuación de los gases perfectos PV = nRT Primer principio dQ = dW + dU = PdV + ncv dT dQ PdV ncv dT nRdV ncv dT = + = + Entropía dS = T T T V T Trabajo Calor TERMODINAMICA Ecuación Relación de Mayer c p − cv = R Coeficiente adiabático γ = Energía interna cp cv Entropía Diagrama Clapeyron ∆S1→2 = nc p L Isóbaro ( dP = 0 ) ( P = Cte ) W1→2 = P(V2 − V1 ) = V1 T1 = V2 T2 Q1→2 = nc p (T2 − T1 ) ∆U 1→2 = ncv (T2 − T1 ) = nR(T2 − T1 ) = nc p L W1→2 = 0 P1 T1 = P2 T2 Q1→2 = ncv (T2 − T1 ) ∆U 1→2 = ncv (T2 − T1 ) = nc v L V Adiabático ( dQ = 0 ) (Q = 0 ) P1 P2 V2 V2 nRT L nRT L W = nRT L = Q = nRT L = → → 1 2 1 2 P1V1 = P2V2 = nRT P2 P2 V1 V1 P1V1γ = P2V2γ T1V1γ −1 = T2V2γ −1 1−γ γ 1 1 TP 1−γ γ 2 = T2 P W1→2 = ncv (T1 − T2 ) = = P2V2 − P1V1 1−γ ∆U 1→2 = 0 = nRL T2 = T1 P P2 P1 ∆S1→2 = nRL Isotermo ( dT = 0 ) ( T = Cte ) P V2 V1 ∆S1→2 = ncv L Isócoro ( dV = 0 ) ( V = Cte ) T2 = T1 V V2 = V1 P P1 P2 V P Q1→2 = 0 ∆U 1→2 = ncv (T2 − T1 ) ∆S1→2 = 0 V