Representación gráfica de procesos de cuasi

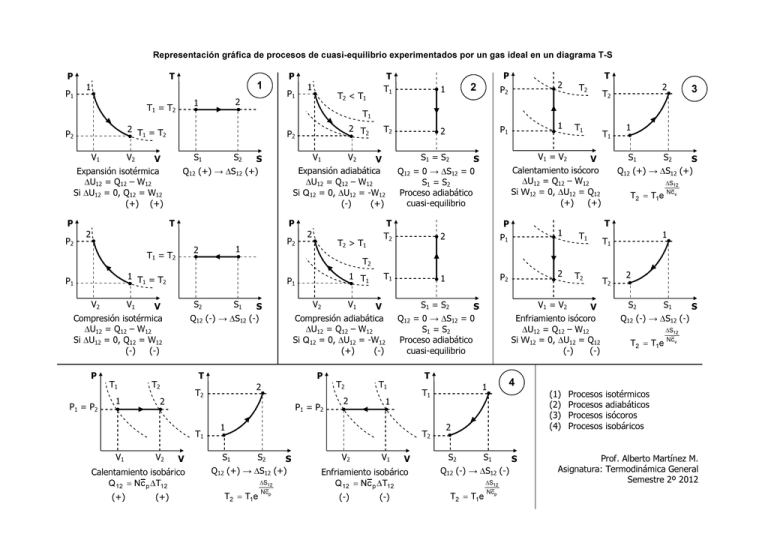
Representación gráfica de procesos de cuasi-equilibrio experimentados por un gas ideal en un diagrama T-S
P
P1
P
T
1
1
V1
S1
V
Expansión isotérmica
∆U12 = Q12 – W12
Si ∆U12 = 0, Q12 = W12
(+) (+)
S2
Q12 (+) → ∆S12
T
T1 = T2
V1
V
Compresión isotérmica
∆U12 = Q12 – W12
Si ∆U12 = 0, Q12 = W12
(-)
(-)
P
P1 = P2
1
P2
1
2
T2
2
V2
V
Calentamiento isobárico
Q 12 = N c p ∆T12
(+)
(+)
2
2
T
2
P2
T2
2
T2
3
2
T2 > T1
1
P1
S1 = S2
T1
T1
V1 = V2
S1
V
Calentamiento isócoro
∆U12 = Q12 – W12
Si W12 = 0, ∆U12 = Q12
(+)
(+)
S
=0
Q12 = 0 → ∆S12
S1 = S2
Proceso adiabático
cuasi-equilibrio
T
T2
2
P1
1
T1
1
P2
2
1
S2
S
Q12 (+) → ∆S12 (+)
T2 = T1e
∆S12
Nc v
T
P
T1
1
T1
T2
1 T1
P1
S2
S1
Q12 (-) → ∆S12
S
(-)
V2
V1
V
Compresión adiabática
∆U12 = Q12 – W12
Si Q12 = 0, ∆U12 = -W12
(+)
(-)
S1 = S2
P1 = P2
2
T1
1
1
T2
S1
S2
S
Q12 (+) → ∆S12 (+)
T2 = T1e
∆S12
Ncp
V2
V1
V
Enfriamiento isobárico
Q 12 = Nc p ∆T12
(-)
(-)
1
T1
S1
Q12 (-) → ∆S12 (-)
T2 = T1e
∆S12
Ncp
2
S2
S1
S
Q12 (-) → ∆S12 (-)
∆S12
T2 = T1e Nc v
4
(1)
(2)
(3)
(4)
2
S2
T2
V
Enfriamiento isócoro
∆U12 = Q12 – W12
Si W12 = 0, ∆U12 = Q12
(-)
(-)
T
T2
T2
V1 = V2
S
=0
Q12 = 0 → ∆S12
S1 = S2
Proceso adiabático
cuasi-equilibrio
P
2
T2
T1
V1
T2
V
Expansión adiabática
∆U12 = Q12 – W12
Si Q12 = 0, ∆U12 = -W12
(-)
(+)
T
T1
1
V2
P
1 T =T
1
2
V2
V1
S
(+)
2
P1
2 T2
P2
V2
P
T2 < T1
P
T
T1
T1
2 T =T
1
2
P2
P2
2
1
T1 = T2
P1
1
S
Procesos
Procesos
Procesos
Procesos
isotérmicos
adiabáticos
isócoros
isobáricos
Prof. Alberto Martínez M.
Asignatura: Termodinámica General
Semestre 2º 2012