Un campo horizontal constante de 0.5 T atraviesa una espira
Anuncio

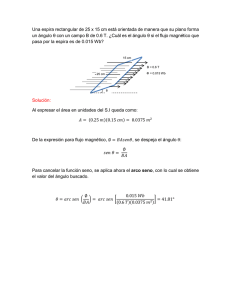
Un campo horizontal constante de 0.5 T atraviesa una espira rectangular de 120 mm de largo y 70 mm de ancho. Determine cuál será el flujo magnético que atraviesa la espira cuando su plano forme los siguientes ángulos con el campo B: 0°, 30°, 60° y 90°. θ Solución: La expresión para determinar la densidad de flujo magnético es: ∅= En este problema no hay que olvidar nuevamente que el área de la espira debe expresarse en m2. Recordando que 1 m = 1000 mm, se tiene que: = (120 ∅= )(70 ) = (0.120 )(0.070 ) = 0.0084 Para un ángulo de 0°: = 0.5 (0.0084 )( 0°) = 0 Note que en este caso el plano es paralelo al campo y por lo tanto, el flujo magnético es nulo debido a que ninguna línea atraviesa el área. ∅= ∅= Para un ángulo de 30°: = 0.5 (0.0084 )( 30°) = 2.1 × 10 )( 60°) = 3.64 × 10 = 2.1 Para un ángulo de 60°: = 0.5 (0.0084 = 3.64 ∅= Para un ángulo de 90°: = 0.5 (0.0084 )( 90°) = 4.2 × 10 = 4.2 Observe que el flujo magnético es máximo cuando el área de la espira es perpendicular al campo magnético, es decir, para θ = 90°.